压力容器是化工、能源等行业中重要的过程设备,具有潜在的泄漏和爆炸危险性[1]。由于其多处在高温高压的服役条件下,盛放的介质具有危害性,在外加应力下内部缺陷区域极易存在应力集中现象,一旦压力容器失效,将会造成重大的经济损失。因此,压力容器必须定期进行在线监测,而无损检测是压力容器监测的有效手段[2]。
传统的无损检测[3-5]虽然能够检测出缺陷位置,但是难以满足智能化、自动化与高精度的多重要求,且存在检测效率低等问题。金属磁记忆检测是一种能够快速便捷定位缺陷的无损检测技术,既可以在役检测出缺陷位置又可以检测出应力集中区域,实现损伤的早期预测和诊断,已在工程中得到部分应用,但是,目前尚缺乏建立磁记忆信号与应力状态之间的定量物理关系[6-7]。
磁记忆信号变化本质上是磁记忆信号与应力集中的关系,因此建立合理的力磁耦合模型,探究铁磁材料的力学性能和磁学性能之间的关系十分必要,国内外学者[8-10]从能量守恒、磁偶极子等不同方向出发进行了研究。近些年来,针对金属磁记忆检测无法实现定量化分析,以至于不能完成缺陷识别的问题,JOSHI等[11]提出用漏磁信号反演三维漏磁信号轮廓,用所得到的结果估计缺陷有效长度、宽度和深度。陈海龙等[12]引入了磁梯度张量,并以磁梯度张量变化来评定损伤区域。罗龙清等[13]具体分析了三维磁记忆信号曲面与疲劳损伤之间的联系。史小东等[14]提出以原始信号能量、中心区域能量、中心区域原始信号突变宽度、平均绝对梯度作为特征值,建立神经网络对缺陷进行分类识别。LI等[15]通过分析磁记忆的谱熵分布来诊断材料中的内应力集中情况,从而监测裂纹扩展。
综上所述,虽然金属磁记忆原理不断完善,但是对于裂纹、凹坑等体积状缺陷的量化分类仍旧存在不足,故需要更加深入地选取具有代表性的特征量[16-17],进而提高金属磁记忆检测量化和识别缺陷的准确性。文章基于三维力磁耦合分析中特征量的选取和分析处理,建立了三维力磁耦合模型,解释三维空间信息在定性和定量分析中的重要性,进一步阐述金属磁记忆检测中静力学与静磁学之间的关系,为金属磁记忆检测缺陷信号的定量和定性分析提供依据。
1. 理论基础
地磁场和外加应力是金属磁记忆检测技术的重要组成部分。处在地磁场环境中的试件受到外力作用时,试件内部不断累加应力能产生局部应力集中区,为平衡内部的能量,其内部磁畴会发生移动或位错。根据最小能量原理,构件能量越低内部晶体结构越稳定,所以磁畴重新排列,通过将应力集中转化成磁弹性能的方式维持内部能量平衡。因此,试件内部产生的磁弹性能和应力集中引起的应力能是相等的。根据能量守恒关系和电磁场理论有

式中:ΔEu为磁能变化量;BT为无外力作用时材料的磁感应强度;Bσ为外应力作用下构件的磁感应强度;H为磁场强度。
由于铁磁构件受到值为σ的载荷,产生的应力能Eσ为

式中:λ为载荷下磁致伸缩系数。
根据能量平衡,得到

式中:,,μ0为真空磁导率;μσ为应力σ时对应的试件磁导率;μT为无外力作用下试件磁导率。
当应力方向与磁化方向平行()时,根据胡克定律,假设铁磁性材料受外力作用下的磁导率呈线性变化,计算公式为[18]

式中:Bm为铁磁材料达到饱和时的磁感应强度;λm为饱和磁致伸缩系数;μ为铁磁材料相对磁导率。
2. 模型和方案
2.1 分析模型
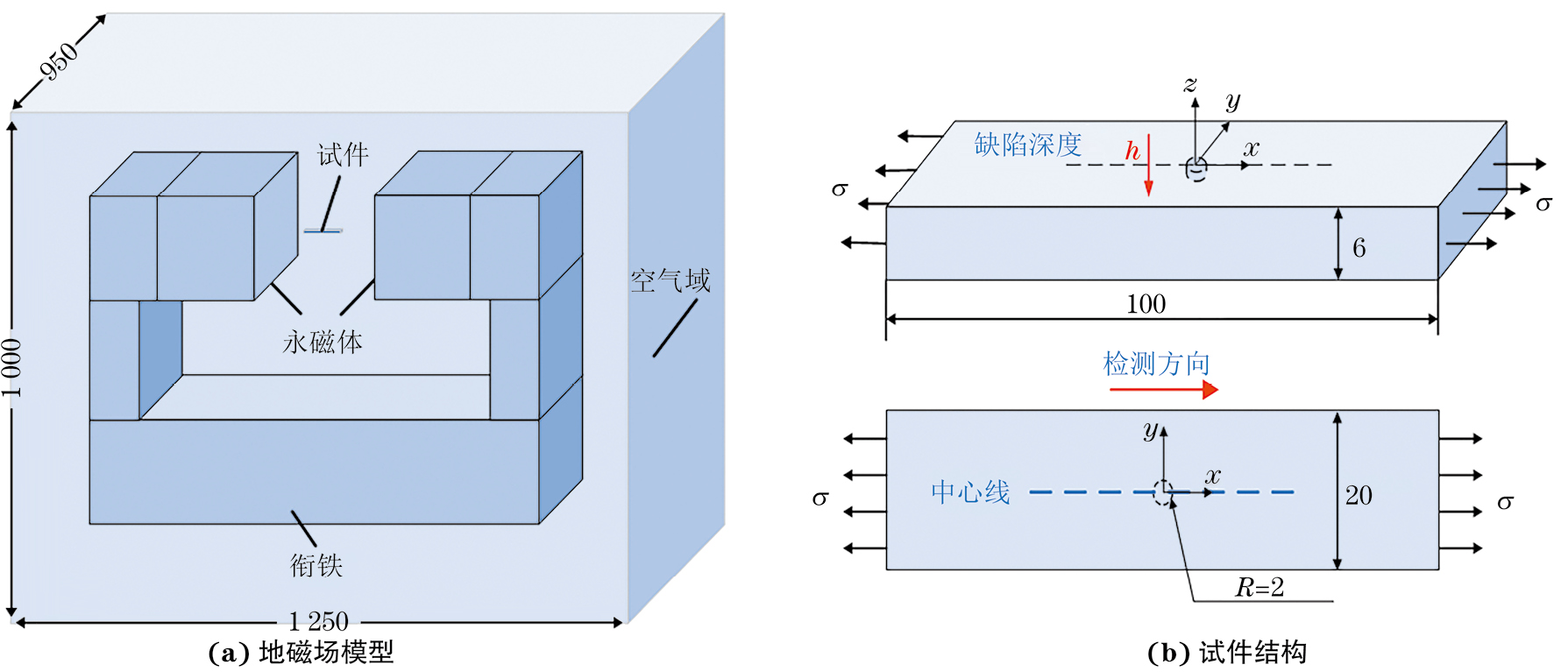
利用“永磁体+衔铁”的形式[19]模拟了处在地磁场环境中的试件磁场强度分布(见图1),衔铁的相对磁导率为186 000[20],建立外部空气层将其包裹,如图1(a)所示。铁磁性试件材料为Q235,试件的尺寸为100 mm×20 mm×6 mm(长×宽×高),在试件中部分别设置圆形凹坑、矩形槽状、气孔三种缺陷。圆孔半径为2 mm,圆孔深度为h,如图1(b)所示。在力学模拟阶段采用SOLID185单元,静磁学模拟阶段采用SOLID96单元,两者都是六面体八节点单元,可以完成力磁耦合时的计算。采用智能网格划分,在试件缺陷位置以及周围将网格进行加密处理,网格尺寸(边长)为0.5 mm,试件位置处磁场强度与地磁场强度值相近,约为40 A·m−1,满足计算要求,可以进行数值模拟计算。
2.2 加载和求解
在静力学阶段,为模拟静载单向拉伸,对含缺陷的试件模型中部进行位移约束,试件两端施加面应力求解,通过力磁关系耦合式[式(4)]计算不同单元中的应力值对应的磁导率值,在后处理模块进行存储。进入静磁学阶段,将数组中各个单元对应的磁导率导入到试件模型中,即,T;;H·m−1;MPa。对最外围空气施加边界条件,运用磁矢量法对分析模型进行磁学加载,即可实现静磁场求解。后处理时,提取路径上各个节点的磁场强度分量即可得到表面漏磁场分布规律[21]。
3. 三维漏磁场特征研究
3.1 凹坑缺陷对磁记忆信号的影响
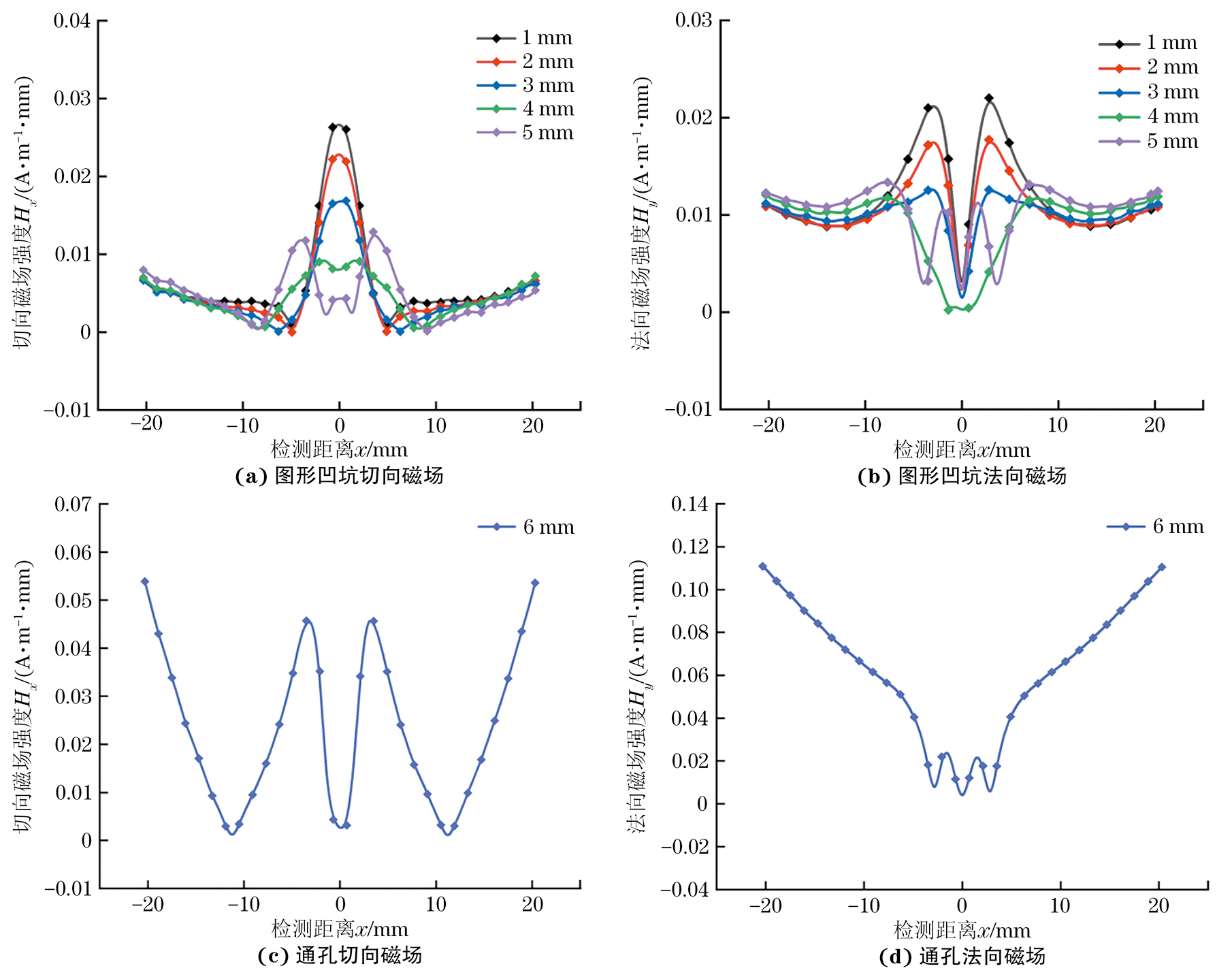
为探究试件在不同缺陷深度下的磁记忆信号规律,采用相同的试件尺寸,改变缺陷深度h,缺陷深度分别为1,2,3,4,5,6 mm时,加载应力为100 MPa,提取距离试件下方1 mm中的空气切向磁场强度和法向磁场强度,提取的路径长度为40 mm,其结果如图2所示。
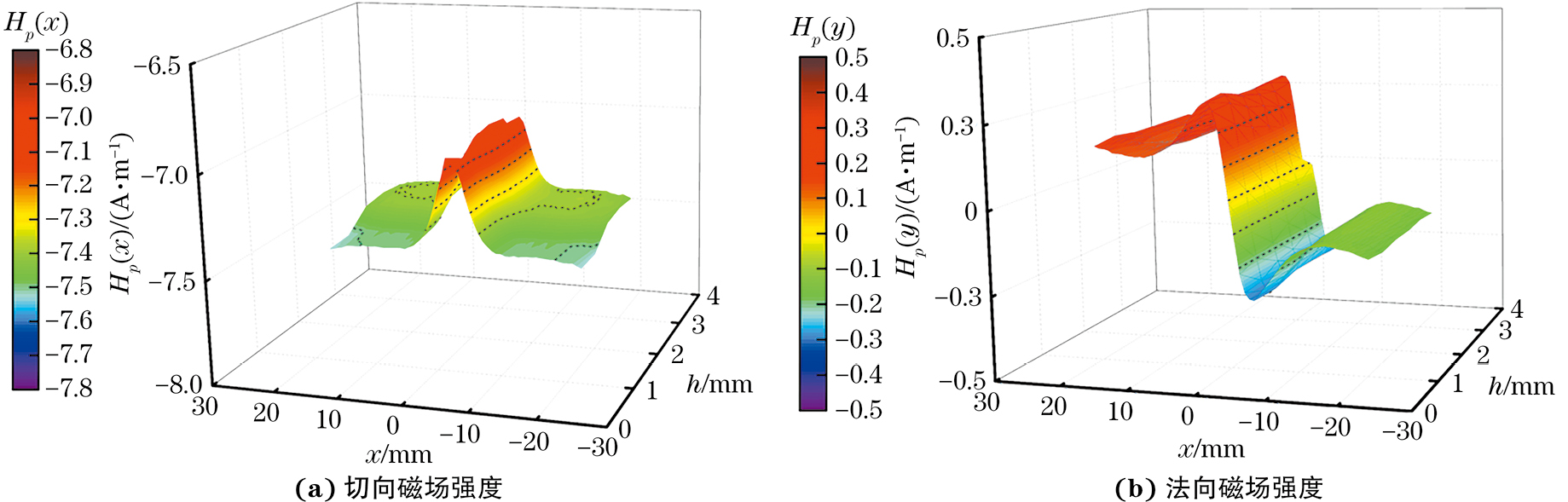
可见,试件尺寸和加载力相同的条件下,当缺陷深度为1~4 mm时,切向磁场强度在缺陷位置处伴有一个极大值出现,法向磁场强度在缺陷处存在异号现象,随着缺陷深度的增加,磁记忆信号逐渐变大,这与文献[22]规律一致。缺陷深度增加到5 mm时,切向磁场强度在缺陷位置周围出现两个极大值和一个极小值。这是因为缺陷变大后试件所能承受的应力减小,为平衡试件内部能量值,磁畴发生磁机械效应,抵消了一部分应力能。随着深度的增加,缺陷变成通孔,于是切向磁场强度和法向磁场强度值急剧增加。根据磁偶极子理论,凹坑缺陷处产生与试件相反极性的磁场,随着缺陷深度的增加,缺陷产生的磁场逐渐增强,磁记忆信号在缺陷处出现“反转”的情况,趋近于通孔的磁场分布,在文献[23]中也出现了同样的现象。为研究圆形凹坑周围的磁场能量变化,对磁记忆信号的切向和法向分量做积分处理[12],其结果如图3所示。
可见,圆孔凹坑缺陷由1 mm扩展至通孔时,切向和法向磁场能量变化大致分为以下三个阶段:①缺陷深度为1~3 mm时,缺陷位置处切向和法向磁场能量逐渐减弱,切向磁场能量具有一个极大值,法向磁场强度具有一个极小值;②缺陷深度为4~5 mm的阶段,缺陷深度为4 mm时,切向磁场强度能量在缺陷位置出现微小波动,法向磁场能量继续减小;缺陷深度增加到5 mm时,切向磁场能量在缺陷处出现明显波动,形状近似“w”形状,法向磁场强度在圆形直径两端出现两个极值;③缺陷变成通孔时,切向和法向磁场能量增强并且波动范围增大。观察总体曲线可知,法向能量幅值在缺陷周围逐渐减小。
3.2 矩形槽缺陷对磁记忆信号的影响
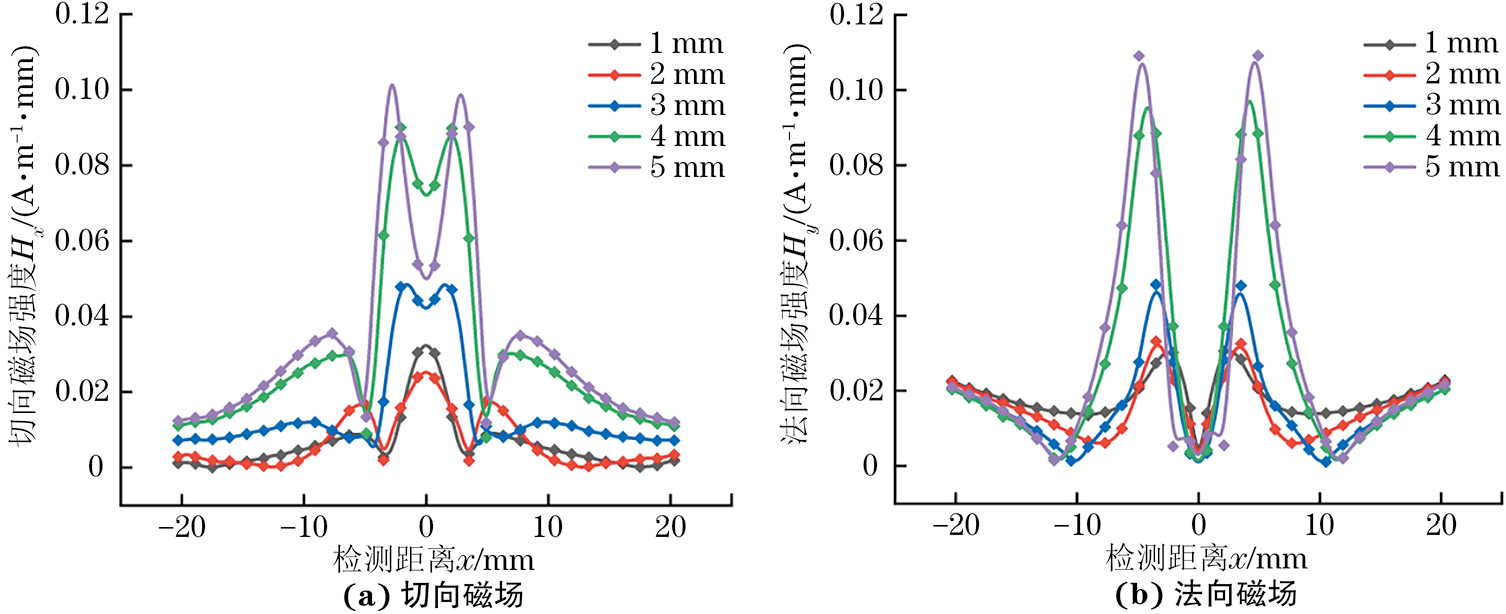
采用相同的地磁场模型和试件,缺陷类型改变为矩形槽状,缺陷深度分别为1,2,3,4,5 mm,缺陷宽度、约束条件与圆孔凹坑的相同。提取到的磁记忆信号如图4所示。
从图4中可以看出,当缺陷深度较小时,磁记忆检测到的信号是由应力集中引起的,切向和法向磁场强度逐渐增加,但是波动范围较小。当缺陷深度增加到试件厚度的50%时,切向和法向分量变化范围显著增大,切向和法向分量能够检测出矩形槽缺陷引起的信号变化,而且曲线出现“反转”现象,其原因与凹坑缺陷信号曲线变化的原因相同;同一槽宽时,随着缺陷深度的增加,磁记忆信号逐渐增大。对磁记忆信号做积分处理,其结果如图5所示。
由图5可知,缺陷深度较小时,切向和法向磁场能量较小,随着缺陷深度增加到试件厚度的50%,切向和法向磁场能量逐渐增加,切向磁场能量在矩形槽中部出现“下凹”现象。而且,随着缺陷深度的增加,矩形槽中部“下凹”变化量增大,法向分量的能量持续增加。观察总体曲线可知,法向能量在缺陷位置一直增加,在缺陷周围呈增加的趋势。与圆孔凹坑相比,矩形槽缺陷磁场能量的幅值较大。
3.3 气孔缺陷对磁记忆信号的影响
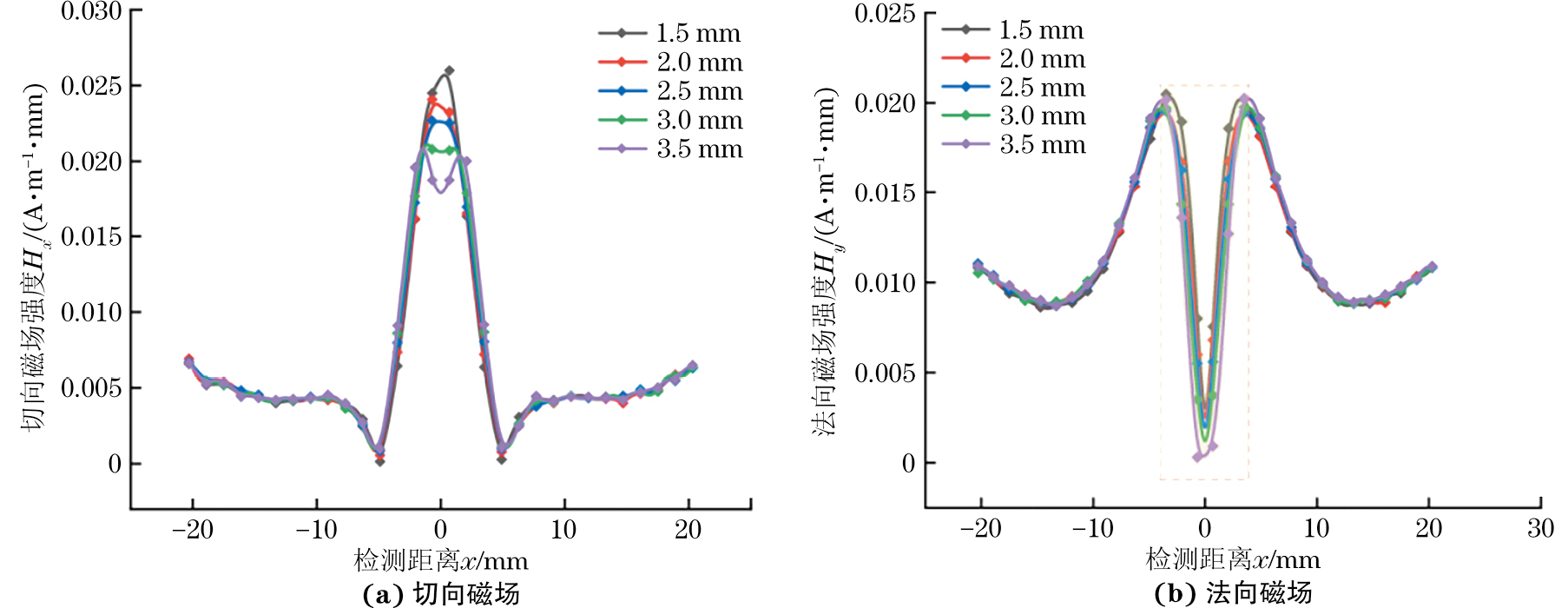
为研究气孔缺陷对磁记忆信号的影响,将气孔缺陷简化为圆球状。气孔半径为1 mm,深度分别为1.5,2,2.5,3,3.5 mm,提取距离试件下方1 mm处的磁记忆信号,其结果如图6所示。
由图6可见,气孔缺陷的切向和法向磁场变化范围较小。在气孔位置处,切向磁场信号出现极大值,法向磁场信号出现过零点现象。随着缺陷深度的增加,切向和法向磁场信号逐渐增强,气孔缺陷左右两端的局部应力集中增强,切向磁场出现“v”形状,法向磁场轮廓波动明显。对磁记忆信号做积分处理,其结果如图7所示。由图7可见,随着气孔深度的增加,切向和法向磁场能量逐渐减小且变化范围较小。当气孔深度为1~2.5 mm时,切向和法向磁场能量变化速率较小,缺陷深度为3~3.5 mm时,变化速率较大。
对于不同的缺陷类型,气孔缺陷的磁场能量变化最小,凹坑缺陷的变化次之,矩形槽缺陷的变化最大。随着缺陷深度的增加,在缺陷位置处,气孔和凹坑缺陷的磁场能量都逐渐减小,矩形槽缺陷的磁场能量逐渐增大,而且能量增加速率变大。数值计算结果表明,不管是圆形凹坑还是矩形槽,缺陷深度低于试件厚度50%时,磁记忆信号对于应力集中引起的信号变化较为敏感。缺陷深度不小于试件厚度的50%时,磁记忆信号能够准确地显示出宏观缺陷的位置,也能体现缺陷引起的局部应力集中。
4. 检测试验制备与试验结果
使用型号为WDW-100G的万能试验机进行静载拉伸试验,型号为EEC-2003+的检测仪进行金属磁记忆检测。磁记忆检测仪选用笔式探头,利用步进电机丝杠组控制探头移动速度和距离,以避免抖动带来的误差。试验开始前先进行参数设置,采用内时钟计时实现脉冲计数,设置“抑制大地磁场”后,再进行大地向上或者向下校准。
采用在线检测的方式,加载的试验力为10 kN,采取力控的加载方式,速度为0.05 kN·s−1。待目标力稳定时,将探头垂直紧贴于试件表面,步进电机带动探头进行移动,探头的移动速度为3 mm·s−1,检测装置与试件如图8所示。试件材料为Q235,选取4个尺寸大小相同的试件,试件的尺寸为100 mm×20 mm×6 mm(长×宽×高),在其中部预制圆孔和矩形槽,缺陷宽度为4 mm,圆孔的深度h分别为1,2,3,4,5 mm,矩形槽的深度h分别为1,2,3,4 mm。
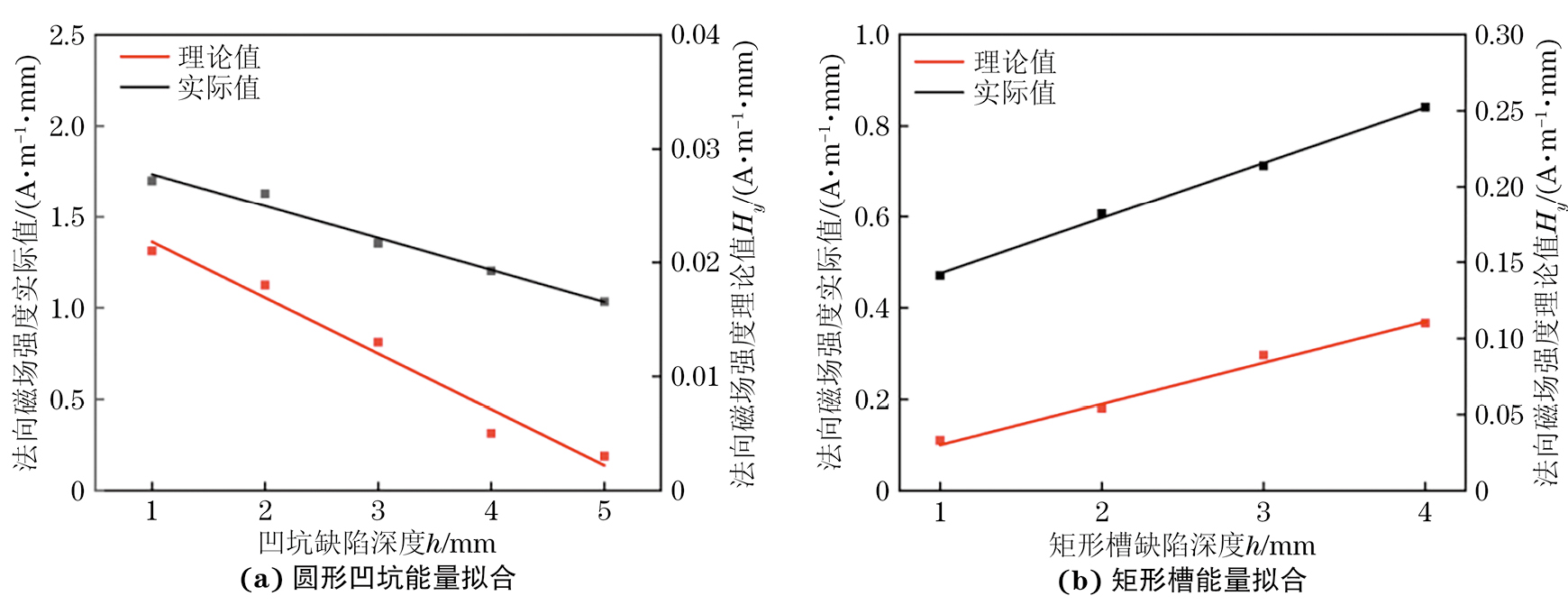
将采集到的法向信号做积分处理后,再对不同缺陷波峰处的法向磁场能量进行拟合并与理论值做对比,拟合结果如图9所示。受试验环境磁场、噪声信号等诸多因素的影响,实际检测的信号比理论信号要大。凹坑缺陷体积比矩形槽缺陷的小,凹坑缺陷能量呈线性变化,有下降趋势;矩形槽缺陷处的能量呈线性变化,有上升趋势。进一步分析来看,凹坑缺陷的理论值拟合公式为y=0.267-0.005x,实际值拟合公式为y=0.912-0.176x。矩形槽缺陷的理论值拟合公式为y=0.003+0.027x,实际值拟合公式为y=0.354+0.122x。对法向信号的拟合分析以及对不同缺陷类型的定量化分析,有助于获取缺陷演变加深过程的信息,从而对缺陷或者应力集中进行监测以及预防。同时,结合神经网络,对特征信号进行处理,也可完成对缺陷类型的识别。
5. BP神经网络模式识别
BP神经网络有较强的学习能力和预测能力,在经过训练后能够对未见过的模式进行正确分类。因此,笔者将BP神经网络与金属磁记忆检测相结合,完成缺陷的智能识别与分类。利用BP神经网络的模型结构,将磁记忆信号的特征量作为输入变量,将不同的缺陷类型作为输出变量,通过学习和训练已知的数据集,对未知的数据进行预测。
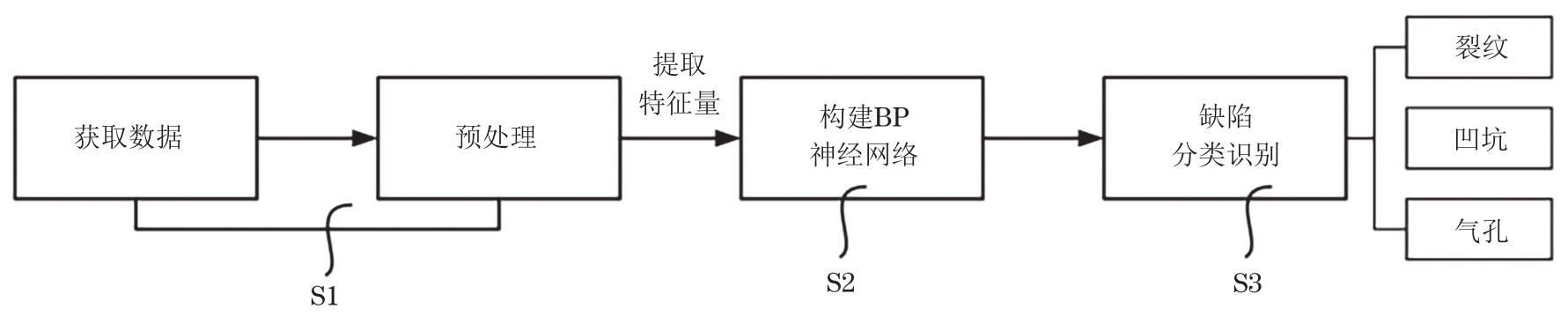
BP神经网络分类识别过程如图10所示,步骤S1,对数值模拟得到的磁记忆信号进行预处理,得到具有代表缺陷特征的参数:缺陷体积V、切向分量波峰-波谷值hp-v、切向磁场梯度Kx、切向磁场能量Hx、法向波峰-波谷值Hp-v、法向分量波宽W、法向磁场梯度Ky、法向磁场能量Hy,然后将此八个参数组成的特征量{V;hp-v;Kx;Hx;Hp-v;W;Ky;Hy}作为输入向量。
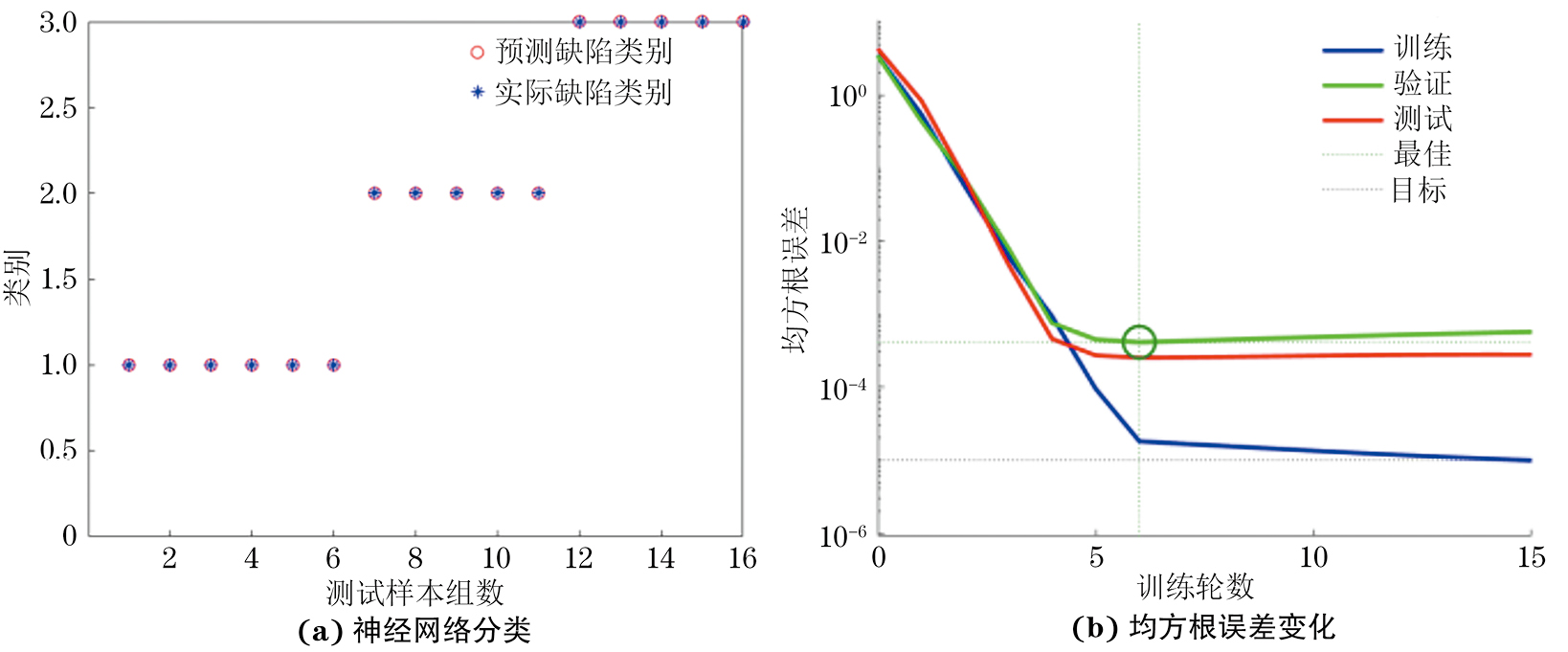
步骤S2为构建BP神经网络。其中,输入的数据集共80组,包括凹坑缺陷30组、裂纹缺陷25组、气孔缺陷25组。首先设置训练数据和预测数据,然后进行参数归一化处理。确定初始的权值和阈值,设置适配参数(训练次数,学习速率,训练目标最小误差等),最后训练神经网络,直至达到最小误差即停止。经训练优化调整,最优的隐含层节点为7个,采用单输出的形式,构建一组3×3的单元向量代替缺陷类型,[1,0,0]代表类别1凹坑缺陷,[0,1,0]代表类别2裂纹缺陷,[0,0,1]代表类别3气孔缺陷,即可完成缺陷识别。缺陷的分类结果如图11所示,可见,搭建的BP神经网络能够100%准确完成缺陷的分类,但是在训练过程中仍然需要有所改进,如图11(b)所示,不断减小均方根误差,提升网络识别的灵敏性和准确性,则可将其应用到实际的工程问题上,从而快速且高效地实现对缺陷信号的分类。
6. 无损检测挂证网结论
文章根据能量守恒和电磁场理论,建立了基于三维力磁耦合分析的压力容器金属磁记忆检测模型,对比分析了不同缺陷类型、缺陷深度的特征信号的变化过程,得到主要结论如下。
(1)圆形凹坑缺陷扩展至通孔时,磁记忆信号逐渐增强,在缺陷处出现“反转”的情况,切向和法向能量先减小后增大;由拟合理论和实际值可得,其法向能量幅值呈线性下降变化。
(2)对于矩形槽缺陷,缺陷深度在试件厚度的50%以下时,应力集中引起的信号变化较为明显,缺陷深度达到试件厚度的50%时,宏观缺陷和应力集中引起的信号变化都有所体现;由拟合理论和实际值可得,其法向能量幅值呈上升线性变化。
(3)随着缺陷深度的增加,气孔缺陷的切向和法向磁场能量逐渐减小,但是对比圆形凹坑和矩形槽来说,其变化范围较小。
(4)在缺陷附近,凹坑缺陷和矩形槽缺陷的磁场能量幅值呈线性变化。采用积分方法分析法向漏磁场能量变化情况具有有效性,可辅助完成缺陷的定性和定量分析。
(5)将金属磁记忆检测技术与BP神经网络相结合,可实现缺陷的智能分类从而既检测出了缺陷位置又检测出了缺陷类型,有效提升了检测效率,节省了检测时间。