随着工业技术的快速发展,对于铁磁性材料的结构完整性和安全性的检测需求越来越高。漏磁检测技术作为一种高效的非破坏性检测方法,已广泛应用于石油化工、能源、制造和运输等行业,用于检测材料中的裂纹、腐蚀等缺陷[1-3]。漏磁无损检测技术基于磁场与缺陷之间的相互作用原理,通过磁化铁磁性试件并测量缺陷处产生的泄漏磁场来进行检测[4-6]。
对于三维信号的分析,主要集中在从复杂的漏磁场信号中准确提取缺陷特征、量化缺陷尺寸,以及在高速检测条件下保持信号的稳定性和准确性等方面[7-9]。WU等[10]分析了均匀和非均匀应力对三维漏磁信号的影响,并设计试验验证了平行和垂直于磁化方向的测量线上的漏磁信号能够描述漏磁场的大小和应力的不均匀性。PIAO等[11]提出了一种基于关键物理参数和最小二乘支持向量机的快速三维缺陷轮廓重建方法,该方法通过贝塞尔曲线模型生成缺陷轮廓,并使用非线性最小二乘方法从三轴漏磁信号中确定局部和全局特征参数,然后采用LS-SVM算法将各个参数进行关联分析,显著提高了现有检测方法的准确性、鲁棒性和计算速度。FANG等[12]提出了一种结合小波散射变换的网络框架,用于估计缺陷宽度,该方法通过提取漏磁信号的特征,并使用神经网络将信号特征映射为缺陷宽度信息,有效提高了小样本数据集上的性能。ZHANG等[13]在线性磁偶极子的理论基础上建立了漏磁场的数值分析模型,并通过三维传感器检测了腐蚀缺陷的漏磁场,为漏磁检测技术提供了数学分析理论。LI等[14]提出了一种结合漏磁检测和磁场扰动的三维重建方法,通过两步策略更新了复杂缺陷的三维重建过程,提高了重建精度。
以上研究多针对矩形槽缺陷,而在实际检测中,圆形开口的平底孔缺陷同样常见。文章分析了两种不同缺陷的三轴漏磁场信号,并结合试验,为不同缺陷漏磁场的三维信号分析和缺陷量化的进一步发展提供理论支持和实践指导。
1. 漏磁无损检测原理
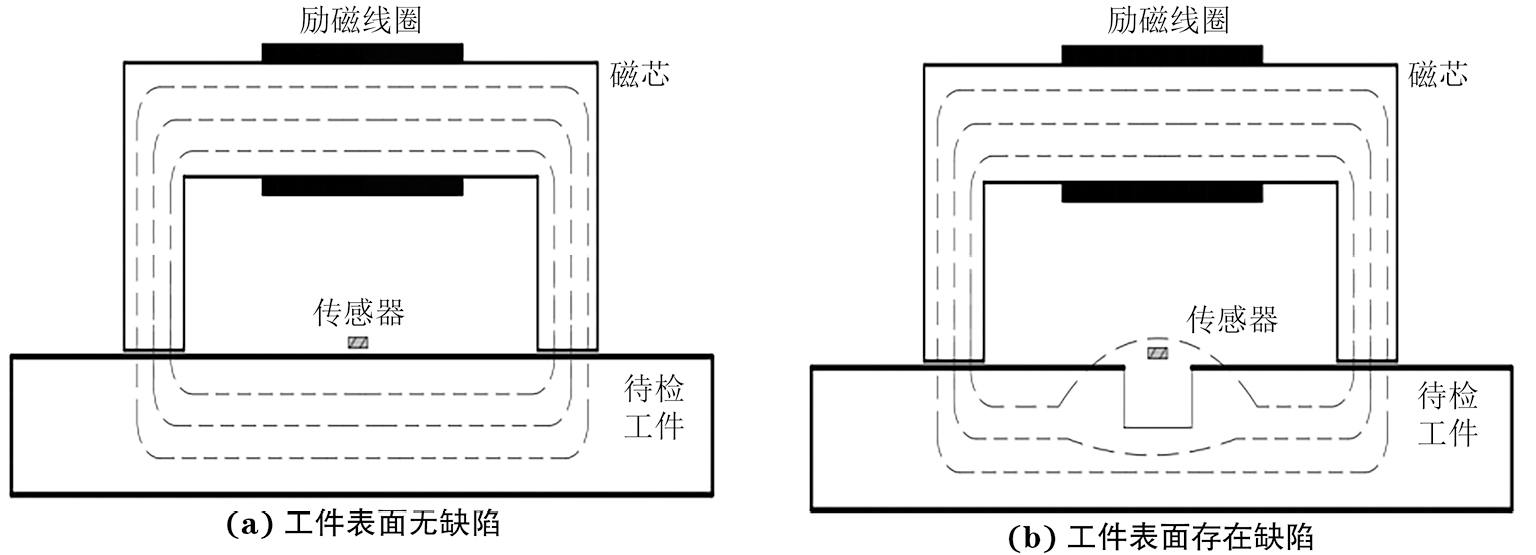
工件表面有无缺陷下的漏磁检测原理示意如图1所示。在励磁源的磁化作用下,励磁装置和待检铁磁性工件形成了闭合磁路。当磁化饱和时,若待检工件材料是均匀连续的,即工件无缺陷,则所有磁力线都被约束在工件内部,且几乎没有磁力线从表面穿出,工件表面几乎没有漏磁场;当被检测工件中存在缺陷时,材料表面的缺陷会使磁导率发生变化,从而增大磁路中的磁阻,使得磁力线的方向和分布发生相应的变化,即磁力线被“挤压”出材料的表面,从而产生可以被检测到的漏磁场,即形成可以检测的漏磁场。
2. 仿真模型建立
在软件COMSOL Multiphysics中建立三维模型,对不同缺陷漏磁场进行仿真分析,使仿真结果更接近实际测量信号。
2.1 三维模型建立
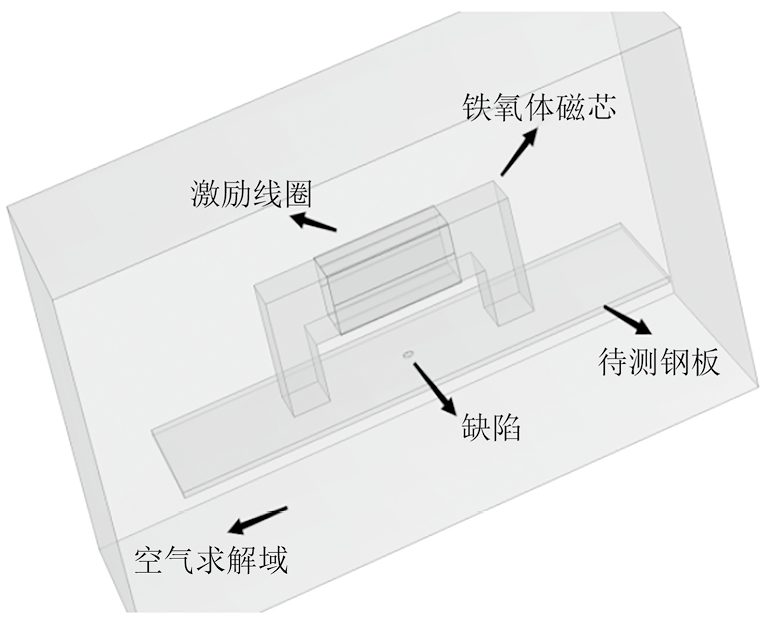
漏磁检测三维模型结构示意如图2所示。使用钢板模拟不同铁磁性构件内壁表面工况,分别建立深度为1 mm,半径为4,5,6 mm的平底孔和尺寸(边长×边长)为4 mm×4 mm,5 mm×5 mm,6 mm×6 mm的矩形槽。各组件材料及几何参数如表1所示。
| 组件名称 | 参数 | |||
|---|---|---|---|---|
| 长度 | 宽度 | 深度 | 材料 | |
| 钢板 | 200 | 120 | 4 | Q235 |
| 磁芯 | 120 | 70 | 30 | 纯铁 |
| 线圈 | 80 | 32 | 2 | 铜 |
| 缺陷 | 4,5,6 | 4,5,6 | 1 | 空气 |
2.2 网格划分
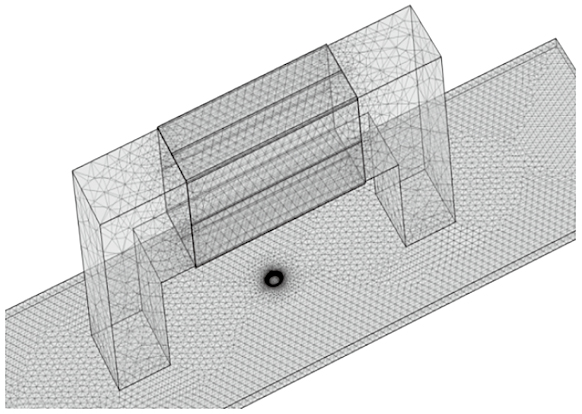
在有限元计算中,网格划分的质量将直接影响计算精度和效率,需要综合考虑网格数量、密度、单元阶次和形状等因素,文章中的模型采用自由四面体网格,并对缺陷周围采用局部网格细化,完整网格包含1 500 528个域单元、95 930个边界单元和 5 092个边单元。网格划分结果如图3所示。
3. 三轴信号特征分析
三轴霍尔传感器将缺陷区域产生的三维漏磁矢量场分解为轴向、径向和周向3个方向。检测时,在贴近待检工件表面的位置布置3个相互垂直的霍尔传感器,分别对应测量漏磁场的轴向、径向和周向分量。这种配置可使检测系统更全面地捕捉和记录缺陷的特征信息,从而显著提高对管道内壁表面缺陷的检测精度,增强缺陷的识别能力。
3.1 轴向信号分析
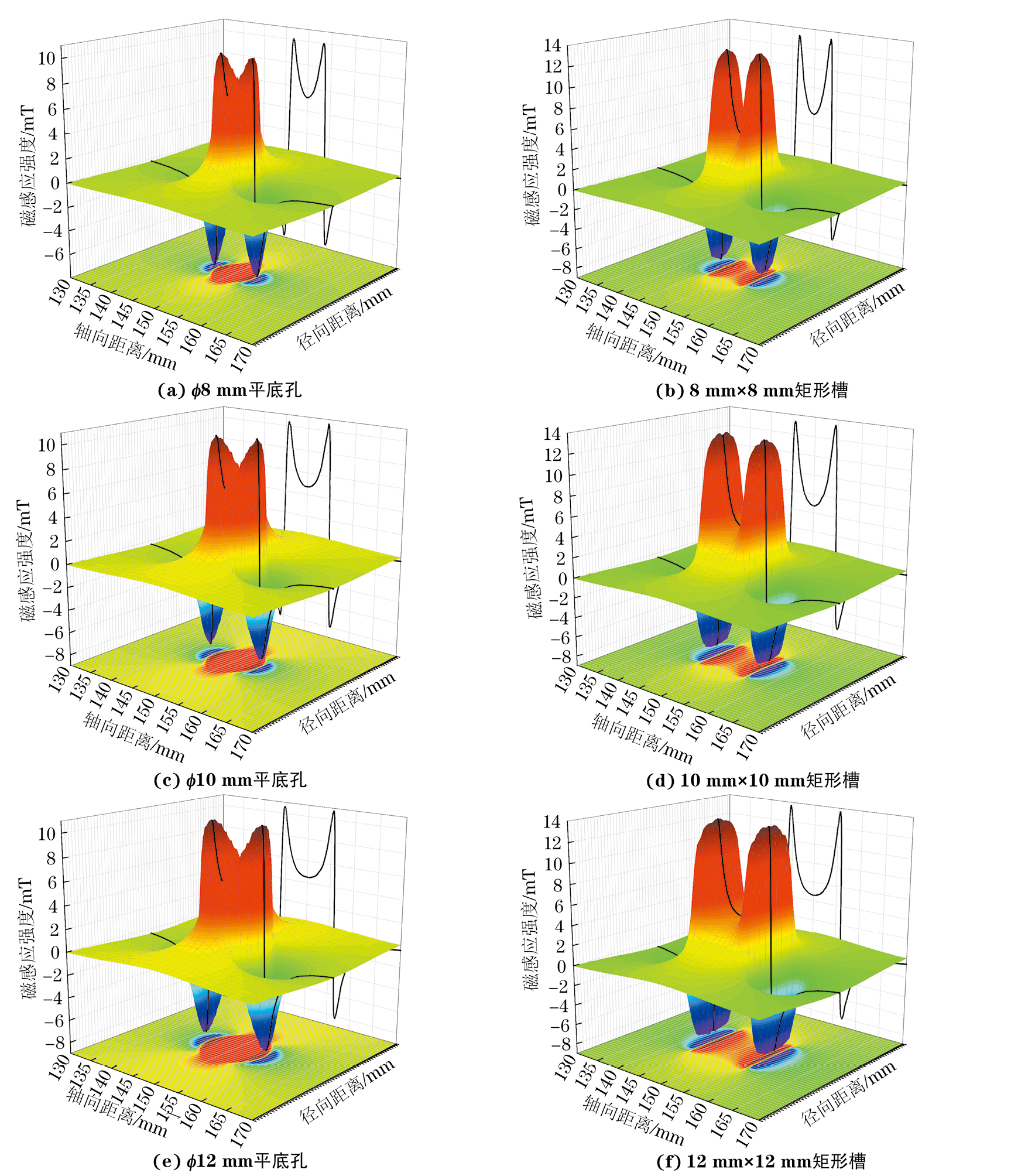
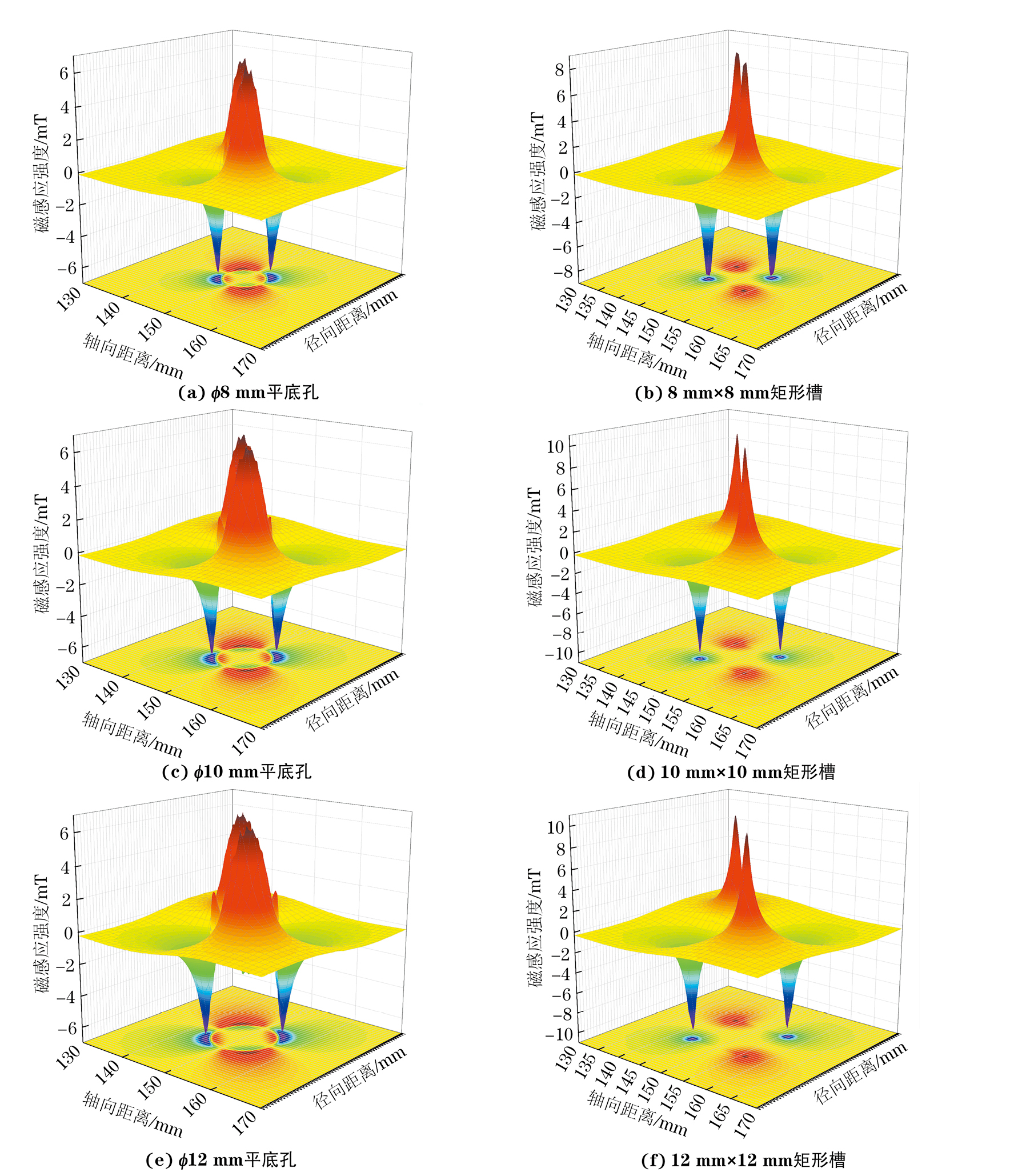
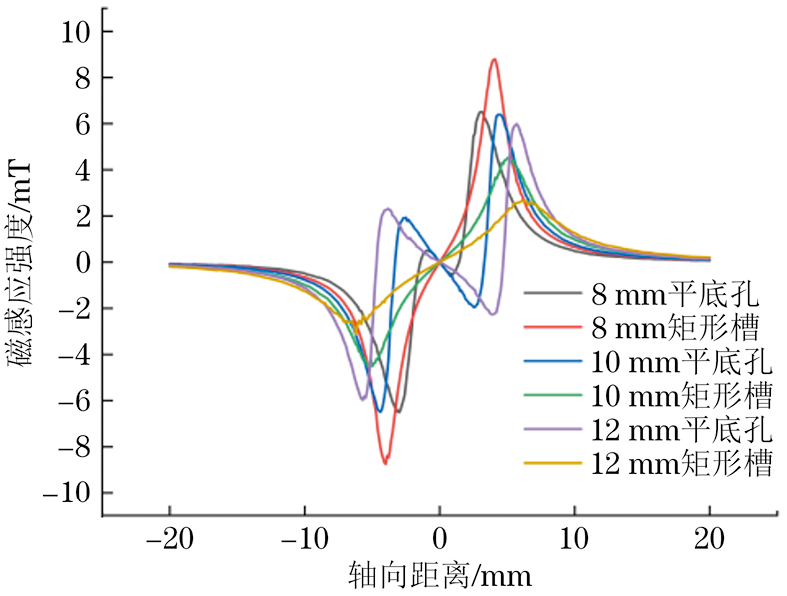
绘制不同缺陷参数特征下平底孔和矩形槽的漏磁场轴向分量,所得漏磁信号如图4所示,可知对于单个缺陷,其信号特征是类似的,即缺陷的轴向分量包含两个较大的正峰值和两个较小的负峰值。对于同类型的缺陷,随着矩形槽缺陷长度和平底孔直径的增大,其峰值也逐渐增大,相同长度和宽度下,矩形槽产生的峰值大于平底孔的,而矩形槽轴向信号形成的峰体积小于平底孔缺陷的。
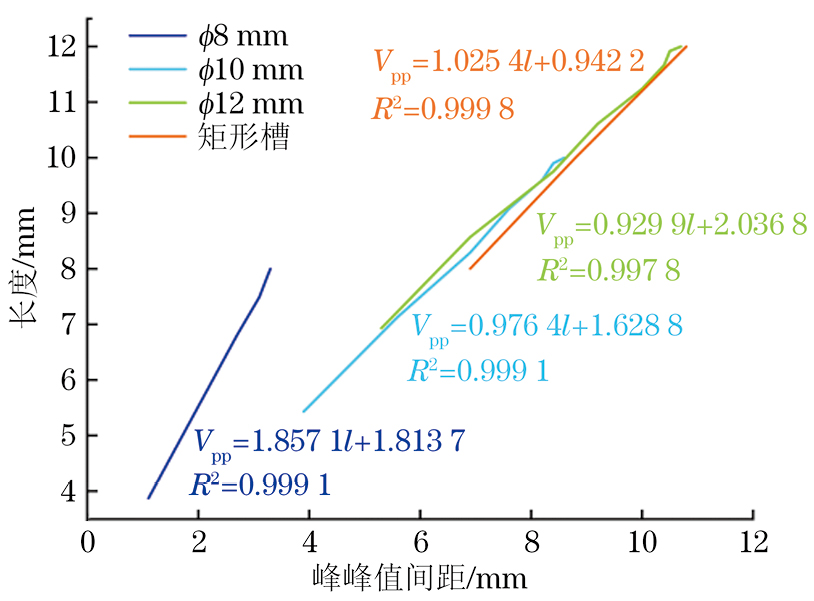
由图4可知,平底孔与矩形槽的缺陷信号在xOz平面上的映射图较为粗略地反映了缺陷的形状特征。一般在进行无损检测的工程适用性评估中,矩形缺陷的轴向信号常用来反映缺陷的深度特征,其峰峰值间距虽然能在一定程度上反映缺陷的长度特征,但是评价结果精确度不高,而圆形开口的缺陷在信号响应上可能展现出与矩形缺陷不同的信号特征。轴向信号图若干通道所测得的峰峰值间距与缺陷实际长度(或平底孔底面的弦长)的关系如表2,3所示,拟合曲线如图5所示(图中Vpp为峰峰值间距,l为缺陷实际长度,R2为拟合精度的判定系数)。
| ϕ8 mm平底孔 | ϕ10 mm平底孔 | ϕ12 mm平底孔 | |||
|---|---|---|---|---|---|
| 峰间距 | 对应弦长 | 峰间距 | 对应弦长 | 峰间距 | 对应弦长 |
| 3.30 | 8.00 | 8.6 | 10.00 | 10.7 | 12.00 |
| 3.25 | 7.88 | 8.4 | 9.90 | 10.5 | 11.92 |
| 3.10 | 7.49 | 8.2 | 9.60 | 10.4 | 11.67 |
| 2.70 | 6.81 | 7.6 | 9.08 | 10.0 | 11.24 |
| 2.10 | 5.71 | 6.9 | 8.29 | 9.2 | 10.61 |
| 1.10 | 3.87 | 5.6 | 7.14 | 8.4 | 9.75 |
| — | — | 3.9 | 5.43 | 6.9 | 8.57 |
| — | — | — | — | 5.3 | 6.93 |
| 8 mm×8 mm矩形槽 | 10 mm×10 mm矩形槽 | 12 mm×12 mm矩形槽 | |||
|---|---|---|---|---|---|
| 峰间距 | 长度 | 峰间距 | 长度 | 峰间距 | 长度 |
| 6.9 | 8 | 8.8 | 10 | 10.8 | 12 |
由图5可知,对于单个平底孔缺陷,轴向信号的峰峰值间距与长度(弦长)之间的数据呈线性关系,拟合程度较好。
3.2 径向信号分析
绘制不同缺陷参数特征下平底孔和矩形槽的漏磁场径向分量,所得漏磁信号如图6所示,可知在平底孔缺陷的漏磁场径向信号分布中,存在一对幅值大致相等的正负双峰,而在矩形槽缺陷信号图中,存在多对此类型的正负双峰。平底孔缺陷由于几何形状的连续性,即圆形弧度的存在,磁力线在其周围重新分布时变化平缓,从而产生缓慢上升和下降的峰值。而矩形槽缺陷边长的统一性使得磁力线在沿边长方向上出现较为一致的重新分布,形成多对的峰值。
平底孔与矩形槽缺陷开口处磁感应强度径向分量分布如图7所示,可知随着矩形槽缺陷长度和平底孔直径的增大,信号的峰值变化较小,主要变化为峰峰值之间距离的增大及峰体积的增大。对于平底孔和矩形槽,直径和宽度及长度相等时,矩形槽产生的漏磁场径向分量峰值大于平底孔的。对于同种缺陷,其峰峰值间距可以清晰反映出缺陷的长度特征,而对于宽度的判定,平底孔的径向信号映射图形构成了一个近似闭合的曲线,而矩形槽的径向信号受到磁化方向的影响,集中于轴向。平底孔缺陷径向信号正峰值随弦长的变化情况如表4所示。
| ϕ8 mm平底孔 | ϕ10 mm平底孔 | ϕ12 mm平底孔 | |||
|---|---|---|---|---|---|
| 峰值/mT | 弦长/mm | 峰值/mT | 弦长/mm | 峰值/mT | 弦长/mm |
| 18.740 | 8.000 | 19.554 | 10.000 | 20.340 | 12.000 |
| 18.584 | 7.877 | 19.448 | 9.902 | 20.270 | 11.920 |
| 17.198 | 7.494 | 18.828 | 9.600 | 19.920 | 11.670 |
| 16.072 | 6.809 | 17.947 | 9.075 | 19.204 | 11.241 |
| 13.673 | 5.713 | 16.246 | 8.285 | 17.927 | 10.613 |
| 9.963 | 3.873 | 14.186 | 7.141 | 16.770 | 9.747 |
| — | — | 11.319 | 5.426 | 14.688 | 8.570 |
| — | — | — | — | 12.177 | 6.925 |
3.3 周向信号分析
绘制不同缺陷参数特征下平底孔和矩形槽的漏磁场周向分量,所得漏磁信号如图8所示,可知,圆形开口缺陷由于几何形状的连续性,对磁场的影响较为均匀,从而在周向上产生对称的多组对称峰值信号。
各缺陷边缘周向信号分量如图9所示,可知磁力线在圆形缺陷周围较为平滑地发生弯曲,产生的磁感应强度相对一致。而矩形缺陷由于其“尖锐”角的存在,在这些角点处会产生更高的磁场梯度,导致磁感应强度在这些区域更为集中,因而映射图中4个峰值点基本对应了矩形槽的4个端点。
4. 检测试验及分析
搭建简易漏磁检测平台(见图10),在钢板试件上加工不同直径的平底孔缺陷和不同边长的矩形槽缺陷。
4.1 轴向信号试验
选取矩形槽、平底孔直径及两条长度不相等的弦长作为检测路径进行试验。
计算不同长度矩形槽及不同直径平底孔缺陷的漏磁信号峰峰值间距Vpp与对应缺陷实际长度l之间的拟合曲线。
直径为8 mm的平底孔拟合曲线为

其中,R2=0.9997。
直径为10 mm的平底孔拟合曲线为

其中,R2=0.9948。
直径为12 mm的平底孔拟合曲线为

其中,R2=0.9776。
矩形槽的平底孔拟合曲线为

其中,R2=0.9999。
不同直径平底孔及不同长度矩形槽缺陷的峰峰值间距与缺陷对应实际长度如表5,6所示,可知,平底孔缺陷的轴向漏磁信号峰峰值间距随着弦长减小而减小,且随着直径增大而增大;相较于平底孔缺陷信号的峰峰值间距与实际弦长的对应关系,矩形槽的峰峰值间距更能反映缺陷的长度,这与仿真分析结果一致。
| ϕ8 mm平底孔 | ϕ10 mm平底孔 | ϕ12 mm平底孔 | |||
|---|---|---|---|---|---|
| 峰间距 | 对应弦长 | 峰间距 | 对应弦长 | 对应弦长 | 峰间距 |
| 3.29 | 8.00 | 5.84 | 10.0 | 9.26 | 12.0 |
| 3.17 | 7.49 | 4.54 | 8.29 | 7.88 | 9.75 |
| 2.71 | 5.71 | 2.87 | 5.43 | 4.82 | 6.93 |
| 8 mm×8 mm矩形槽 | 10 mm×10 mm矩形槽 | 12 mm×12 mm矩形槽 | |||
|---|---|---|---|---|---|
| 峰间距 | 长度 | 峰间距 | 长度 | 长度 | 峰间距 |
| 6.12 | 8 | 7.96 | 10 | 9.79 | 12 |
4.2 径向信号试验
平底孔缺陷的径向信号正峰值对应弦长如表7所示,可知平底孔缺陷的径向漏磁信号正峰值随着弦长减小而减小,且随着直径增大而增大,与仿真分析结果相符。
| ϕ8 mm平底孔 | ϕ10 mm平底孔 | ϕ12 mm平底孔 | |||
|---|---|---|---|---|---|
| 峰值/mT | 弦长/mm | 峰值/mT | 弦长/mm | 峰值/mT | 弦长/mm |
| 2.55 | 8.00 | 2.69 | 10.00 | 2.92 | 12.00 |
| 2.48 | 7.49 | 2.56 | 8.29 | 2.60 | 9.75 |
| 2.19 | 5.71 | 2.01 | 5.43 | 2.16 | 6.93 |
5. 无损检测挂证网结论
通过仿真模拟和试验对管道内壁表面常见的平底孔和矩形槽缺陷的漏磁场三轴信号分布进行了分析,得出以下结论。
(1)对于不同缺陷类型,轴向信号可以粗略反映缺陷长度;径向信号的映射云图能较好描述平底孔缺陷开口形状的轮廓,而对于矩形槽的周向边缘轮廓反映不清晰;不同缺陷类型的周向信号形成的峰体积相差较大,信号的映射云图能较好描述平底孔缺陷开口形状的轮廓,而矩形槽缺陷信号映射图只反映了顶点的位置。
(2)对于平底孔缺陷,不同弦长的扫查路径所得到的轴向漏磁信号的峰峰值间距会随着弦长减小而衰减,其关系满足拟合程度较好的线性关系;矩形槽缺陷长度和轴向漏磁信号的峰峰值间距拟合程度相较于平底孔的更好
推荐阅读: