阵列天线在实际服役过程中,长期暴露在户外环境中,其结构易受温度、风荷等因素影响而发生阵面变形。天线变形不仅易造成天线结构损坏,而且会引起天线阵元之间的相对位置产生偏移误差,造成阵列天线的辐射方向发生变化,从而影响天线的工作性能。此外,近年来阵列天线正在朝大口径方向发展[1],庞大的阵列单元更会加剧阵面变形带来的位置误差。因此,为了保证阵列天线的正常运行,需要对天线阵面变形造成的误差进行补偿校正[2],而实现补偿校正的前提是获取可靠的天线阵面变形信息。
目前,阵列天线变形的监测方法大多为接触式监测法,即通过应变传感器获取结构表面的应变信息,结合变形重构算法实现结构变形的实时感知。现有的变形重构算法包括曲率递推算法、模态法、KO位移理论和逆有限元法。其中,逆有限元法具有不受材料特性和载荷分布影响、重构精度高的优势,逐渐成为变形重构算法的首选。自TESSLER等[3]于2004年首次提出三节点逆有限板单元后,学者们[4]针对不同结构,开发出四节点板单元、八节点壳单元等离散单元,并将其应用于船体甲板[5]、机翼[6]、天线阵面[7]等结构中。如KEFAL等[8]分别于2016年和2019年开发了四节点四边形反壳单元iQS4和八节点曲面反壳单元iCS8,并通过数值仿真和试验验证了iQS4单元和iCS8单元对复杂结构的适用性。而为了保证逆有限元法在结构变形中的重构精度,需要在结构表面进行大量传感器的布设,增加了监测成本。针对这一问题,GHASEMZADEH等[9]将遗传算法引入到逆有限元法中,以优化板壳结构的传感器布局模型。但是上述方法需要事先确定传感器数量,即在传感点数量确定的前提下寻找传感器最优布设位置,从而导致无法得到最优的传感器数量。
基于上述背景,文章提出了一种基于改进逆有限元法的阵列天线变形监测方法,利用多目标遗传算法改进逆有限元法,对算法精度和传感器数量进行双目标优化。并通过算法仿真测试和试验验证了改进逆有限元法对重构精度和传感器数量双目标优化的有效性。
1. 阵列天线变形重构方法
1.1 逆有限元法原理
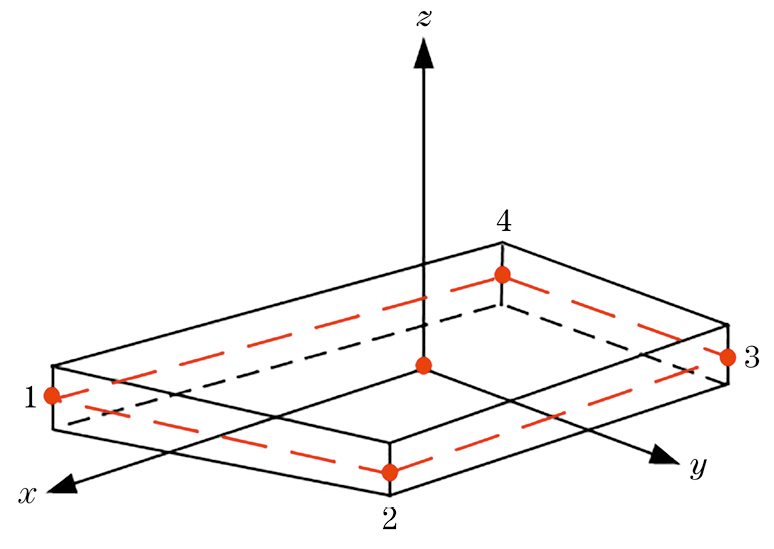
逆有限元法是一种基于板壳弹性变形理论和有限元离散思想的应变-位移反演算法,主要目的是利用离散应变反演出结构单元位移场。根据天线阵面板状结构形式,文章构建的四节点四边形板单元结构示意如图1所示。该逆向单元以板单元的质心为原点建立局部坐标系,以平板中性层作为基准面,单元沿x、y、z方向的长度分别为2a、2b、2h。
根据一阶剪切变形理论,板单元内任一点的位移可以表示为

式中:ux、uy和uz分别为板单元内部一点沿x、y、z方向的位移;u、v和w分别为平板中性层沿着x、y、z轴方向的位移;θx和θy分别为平板中性层绕x轴和y轴的转角。
板单元内任意一点的自由度可以通过单元节点自由度与单元形函数相结合来共同表示。
根据线性弹性理论可知,任一点处的应变可由单元节点位移矢量表示,即

式中:、分别为节点沿x、y方向的线应变;γxy、γxz、γyz分别节点为沿xoy平面、xoz平面、yoz平面的切应变;、k(ue)、g(ue)分别为单元膜应变、弯曲应变和横向剪切应变;Bm、Bb、Bs分别为膜应变转换矩阵、弯曲应变矩阵和剪切应变矩阵,其代表各类应变与单元节点位移向量之间的矩阵关系;ue为逆向单元节点位移矢量,由4个节点的位移向量ue1、ue2、ue3、ue4构成,则有

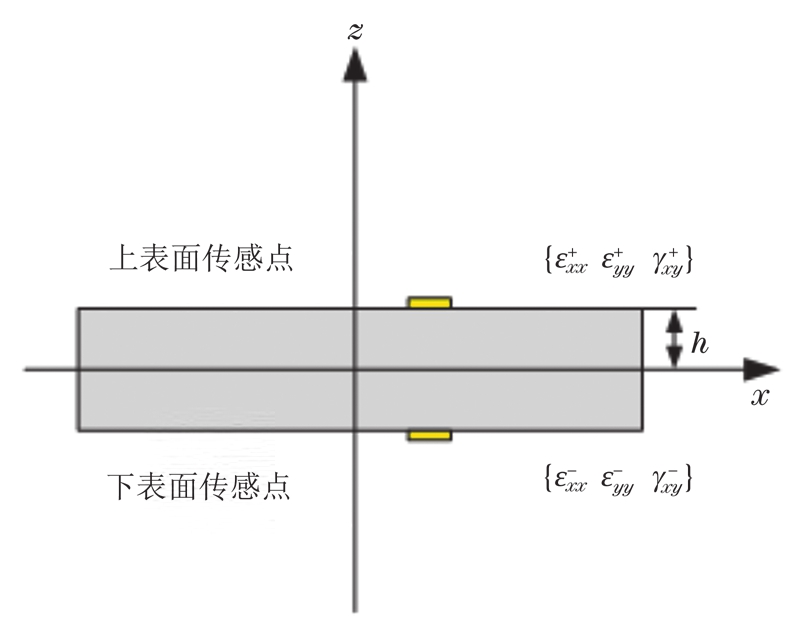
上述的应变转换矩阵反映了单元理论应变,为了获取逆向单元的实际应变值,需将应变传感器布设于板单元的上下两侧,布设图如图2所示(图中h为1/2板厚)。由于平板实际变形时,横向剪切应变相比于膜应变和弯曲应变而言非常小,因此,单元的实测应变只考虑膜应变与弯曲应变的测量值,关系分别为

为求解单元应变与位移的转换关系,逆有限元法基于加权最小二乘函数建立了单元理论应变与实测应变之间的误差函数。根据上述分析,每个逆向单元的理论应变会包括膜应变、弯曲应变和剪切应变,其误差函数为

式中:ωb、ωm、ωg分别为与膜应变、弯曲应变以及剪切应变相关的无量纲加权系数,用以衡量各应变对结构变形的贡献量;∈为实测膜应变;k为实测弯曲应变;g为实测横向剪切应变。
当应变传感器无法监测应变信息导致实际应变数据缺失时,对应的加权系数取极小值10−5。对上述误差函数关于节点位移ue求偏导,并令其为零,可得到该误差函数的最小值,即

式中:ke为伪刚度矩阵;fe为伪载荷向量;ue为待求变形位移量;Bs为剪切应变矩阵;Bm为膜应变转换矩阵;Bb为弯曲应变矩阵;T为矩阵转置符号;h为1/2板厚。
1.2 算法仿真测试
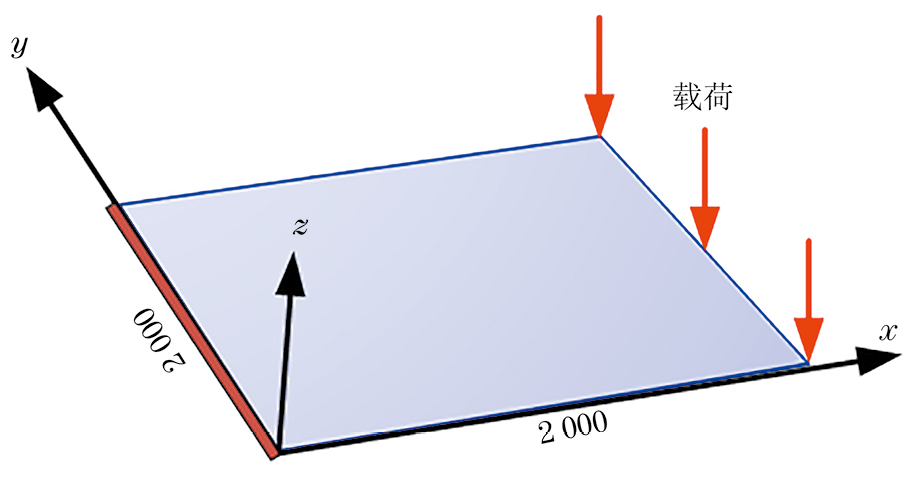
为研究逆有限元算法的重构精度,笔者利用静态载荷下的悬臂板模型进行仿真分析。基于COMSOL软件建立如图3所示的悬臂板仿真模型用以模拟阵列天线。悬臂板的尺寸为长2 000 mm、宽2 000 mm、厚5 mm。板的材料选择为铝,其密度为2 700 kg·m−3,杨氏模量为70 GPa,泊松比为0.33。
对上述仿真模型沿z方向施加静态载荷,使悬臂板模型发生弯曲变形。采集模型中各逆向单元中心点的应变值,将其作为单元理论应变值输入到逆有限元法中,可得到单元节点位移的算法重构值。将悬臂板仿真模型中的单元节点仿真位移值作为实际位移值,以节点位移相对误差表示算法的重构精度,w表示算法重构位移值,w'表示仿真位移值,则有

为验证逆有限元算法的重构精度,分别将悬臂板划分成(行×列)2×2,3×3,6×6的单元,在不同的单元划分下施加相同载荷进行位移重构,其结果如表1~3所示。
| 节点编号 | w/mm | w'/mm | 相对误差error |
|---|---|---|---|
| 1 | 1.529 | 1.663 | 8.10% |
| 2 | 1.607 | 1.711 | 6.08% |
| 3 | 1.528 | 1.663 | 8.12% |
| 4 | 0.408 | 0.484 | 15.70% |
| 5 | 0.483 | 0.537 | 10.10% |
| 6 | 0.410 | 0.484 | 15.29% |
| 节点编号 | w/mm | w'/mm | 相对误差error |
|---|---|---|---|
| 1 | 1.611 | 1.663 | 3.13% |
| 2 | 1.657 | 1.705 | 2.82% |
| 3 | 1.657 | 1.705 | 2.82% |
| 4 | 1.611 | 1.663 | 3.13% |
| 5 | 0.802 | 0.834 | 3.84% |
| 6 | 0.850 | 0.882 | 3.63% |
| 7 | 0.849 | 0.882 | 3.63% |
| 8 | 0.802 | 0.834 | 3.84% |
| 9 | 0.197 | 0.213 | 7.51% |
| 10 | 0.239 | 0.254 | 5.91% |
| 11 | 0.239 | 0.254 | 5.91% |
| 12 | 0.197 | 0.213 | 7.51% |
| 节点编号 | w/mm | w'/mm | 相对误差error |
|---|---|---|---|
| 1 | 1.646 | 1.663 | 1.02% |
| 7 | 1.648 | 1.663 | 0.90% |
| 12 | 1.273 | 1.280 | 0.55% |
| 17 | 0.872 | 0.882 | 1.15% |
| 21 | 0.829 | 0.834 | 0.60% |
| 24 | 0.526 | 0.533 | 1.31% |
| 27 | 0.513 | 0.519 | 1.16% |
| 31 | 0.249 | 0.254 | 1.97% |
| 34 | 0.240 | 0.243 | 1.23% |
| 38 | 0.066 | 0.068 | 2.94% |
| 40 | 0.066 | 0.068 | 2.94% |
| 41 | 0.064 | 0.066 | 3.03% |
由算法验证可得,在2×2单元划分方案下,算法最大相对误差达到了15.32%,而在3×3与6×6单元划分方案下,最大相对误差分别为7.51%和3.03%,表明节点的位移重构误差与单元网格数量有明显的关系。随着板划分单元网格的细化,逆有限元法的重构精度也会显著提高,但同时也带来了应变传感器布设数量的增加以及算法位移重构效率的下降。
2. 多目标遗传算法改进逆有限元法
2.1 多目标遗传算法改进原理
在工程应用中,如何在保证重构精度的同时尽可能减少应变传感器的数量是需要研究的问题,这实际上是一个多目标优化问题。工程上常引入“帕累托(Pareto)最优解”来描述多目标优化问题中的最优解。一般来说,Pareto最优解并不唯一,多目标优化问题的核心就是寻找一组Pareto最优解集,称之为Pareto前沿,其表示了最优解在各目标之间的最佳权衡。
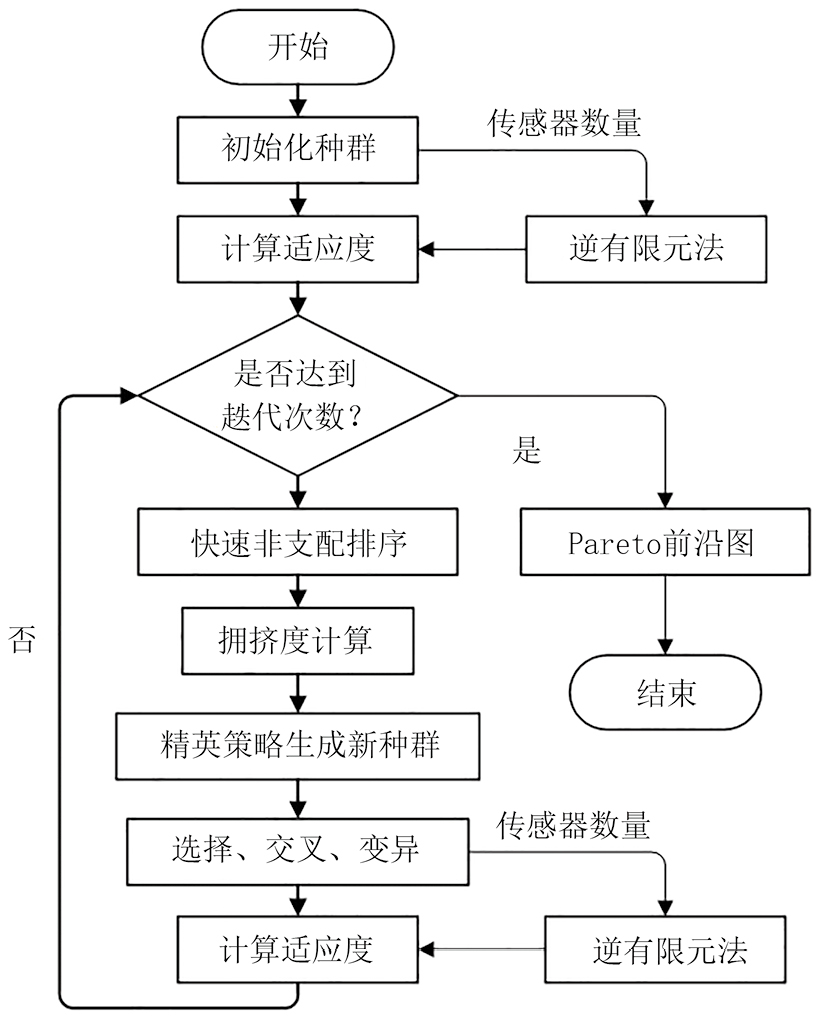
快速非支配排序遗传算法(NSGA-II)是一种基于Pareto最优解的多目标遗传算法,常被应用于各种多目标优化问题。该算法在基本遗传算法的基础上,加入了快速非支配排序和计算拥挤度距离两个模块,对种群中的每个个体进行多次选择和繁殖,具备高效性和稳定性的优点。NSGA-II算法将传感器数量信息输入到逆有限元法中,并获取该数量下的位移重构误差,从而对重构误差与传感器数量进行双目标优化,优化流程如图4所示。
2.2 改进算法的目标函数
根据上述改进算法原理,文章针对算法重构精度和应变传感器数量建立了相对应的适应度函数。其中为了评价算法重构精度,以有限元仿真位移值作为真值,引入均方根误差作为算法重构精度的适应度函数,其中,wi为算法重构的板单元节点的位移值,wi'为COMSOL仿真软件计算出的单元节点位移值,具体如下

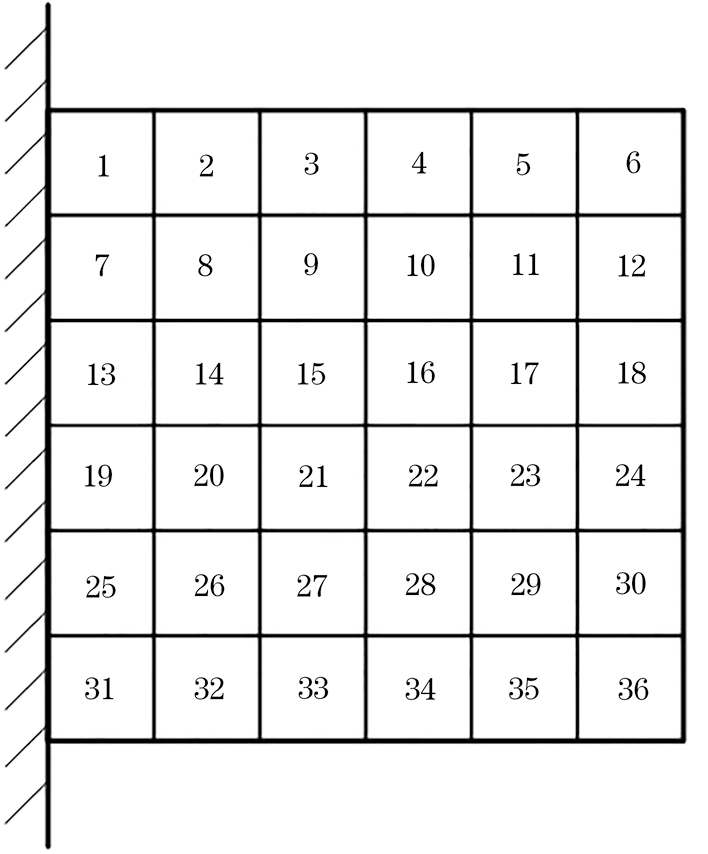
为了分析应变传感器的数量信息对重构算法的影响,将板划分成6×6单元,36个单元的编号示意如图5所示。文章将每一种布设方式初始化为二进制编码,利用布尔矩阵保存每个个体的二进制编码,其中有布设传感器的单元位置为1,未布设传感器的单元位置为0,将所有个体的布尔矩阵值用数组L(x)存储。因此,只需统计出数组L(x)中数值为1的数量即为应变传感器的数量,m(x)为其适应度函数,sum(x)函数表示统计数组中数值为1的数量。
则,改进算法的双目标函数如下

式中,N+为正整数。
2.3 改进算法仿真测试
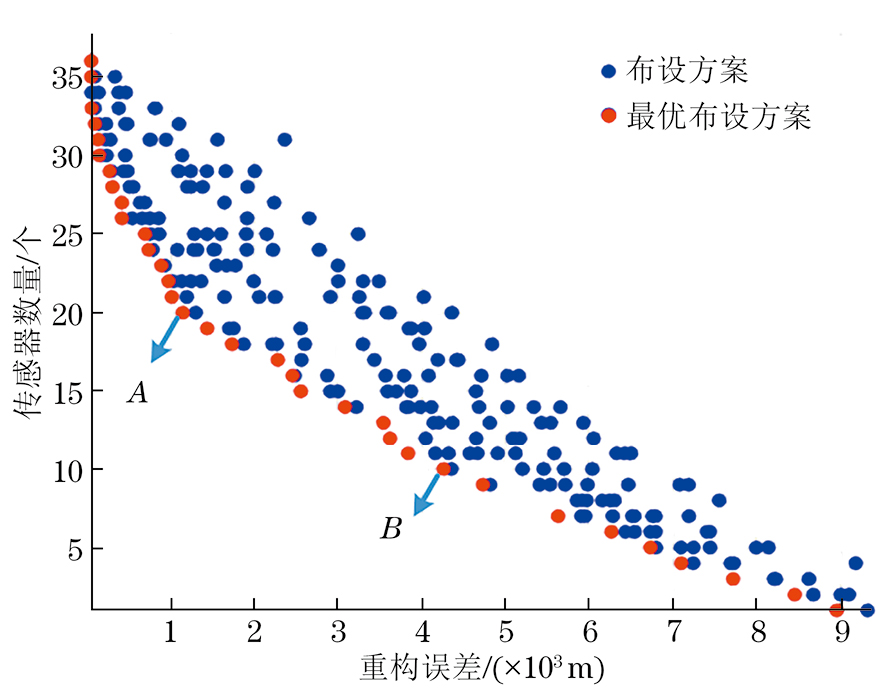
文章根据式(13)建立双目标函数后,在上述划分的6×6板单元上运用改进逆有限元法进行变形监测。为防止优化算法早熟收敛,设置种群数量为50,迭代次数为50,最后得到36单元下算法重构精度与传感器数量的双目标优化结果(见图6)。
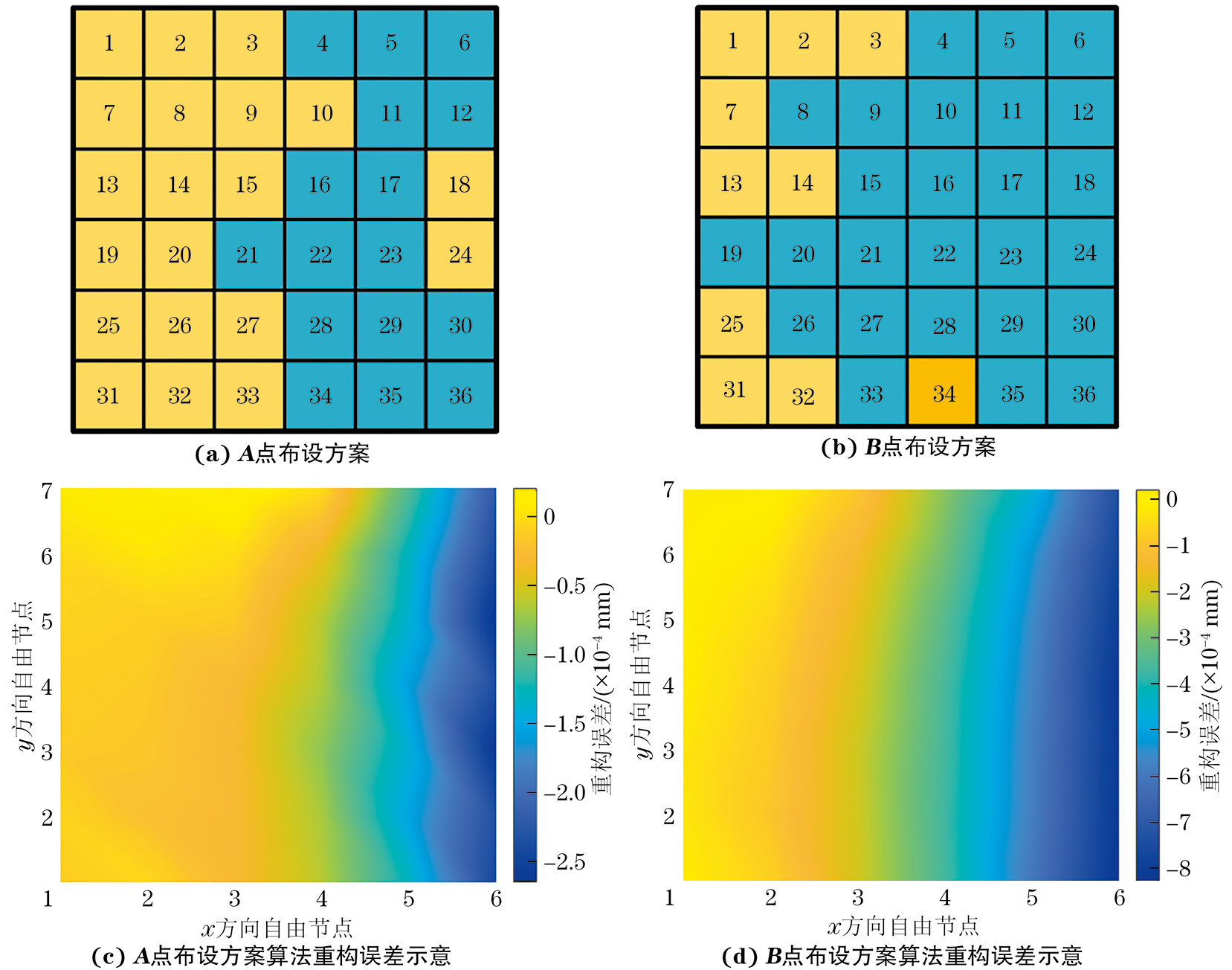
图6中横轴表示算法位移重构的均方根误差,纵轴表示应变传感器数量,红色各点均为双目标优化后的Pareto最优解。从图6中可以看出,Pareto最优解集呈现出明显的负相关趋势,即随着应变传感器数量的增加,算法重构的均方根误差函数也逐渐变小,表明算法重构精度逐渐提高。分别取图6中A、B两点所代表的数据,将其传感器布设方案代入到逆有限元法中,可得出A、B两点的布设方案图和位移重构误差,其结果如图7所示,其中黄色代表选择的单元位置,蓝色代表未被选中的单元位置。
根据上述重构结果可知,A点代表的布设方式为36个板单元中取20个单元进行传感器布设,算法重构的均方根误差为1.147 mm,最大重构误差为0.272 mm。B点代表的布设方式为36个板单元中取10个单元进行传感器布设,算法重构的均方根误差为4.264 mm,最大重构误差为0.828 mm。综合重构精度和传感器数量,A点代表的布设方案的重构精度约为B点的4倍,而前者布设的传感器数量仅为后者的两倍,这表明在一定范围内,增加传感器数量可以显著提高算法重构精度,在实际情况中,应根据传感器布设难度和重构误差允许范围,综合选择布设方案。
3. 试验验证
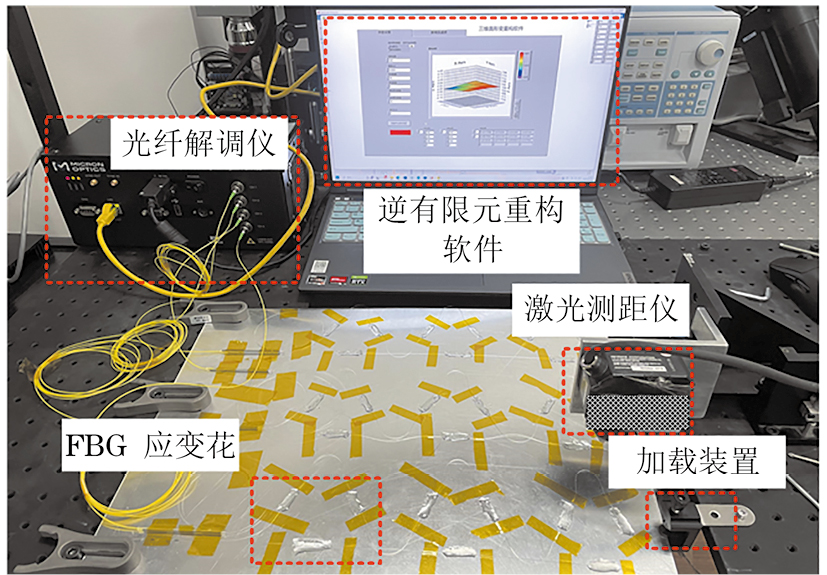
通过上述对改进逆有限元法的仿真测试,初步验证了算法的位移重构效果,文章进一步开展试验以验证算法在实际环境下的效果。受制于试验环境,文章以铝板模拟阵列天线,铝板的长度为40 cm,宽度为30 cm,厚度为2 mm。变形监测试验平台实物如图8所示,包括待测铝板、光纤光栅(FBG)应变花、光纤解调仪、逆有限元重构软件、加载装置以及激光测距仪。
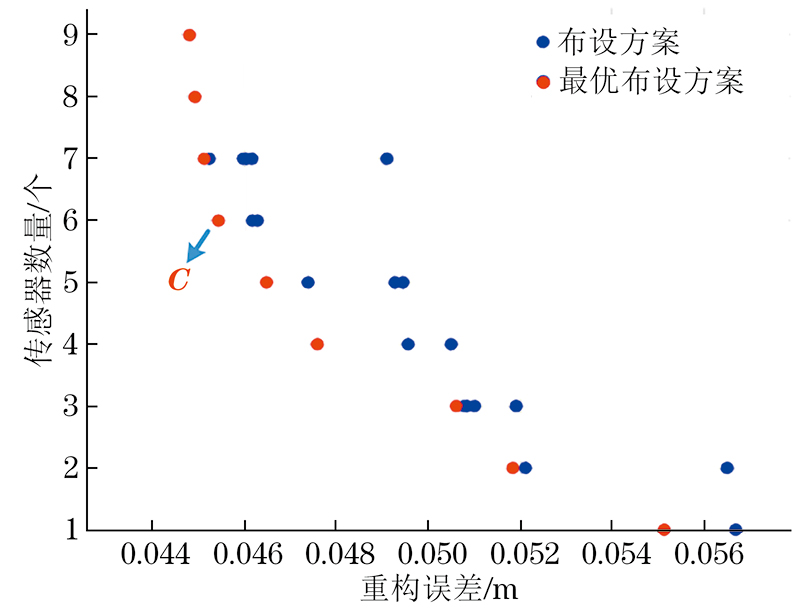
由于铝板尺寸较小,笔者将铝板进行3×3网格划分,共9个逆向单元。每个逆向单元的尺寸为10 cm×10 cm。在试验过程中,将铝板一端作为固定约束,另一端利用加载装置施加静态载荷。通过逆有限元重构软件获取算法的重构位移值,同时使用激光测距仪对铝板上的单元节点进行测量,并将其测量值作为真实值分析算法在实际环境中的位移重构效果。为了在保证算法重构精度的同时尽量减少应变传感器的布设数量,笔者在3×3逆向单元上利用上述基于多目标遗传算法改进的逆有限元法进行重构精度和应变传感器数量的多目标优化,优化结果如图9所示。
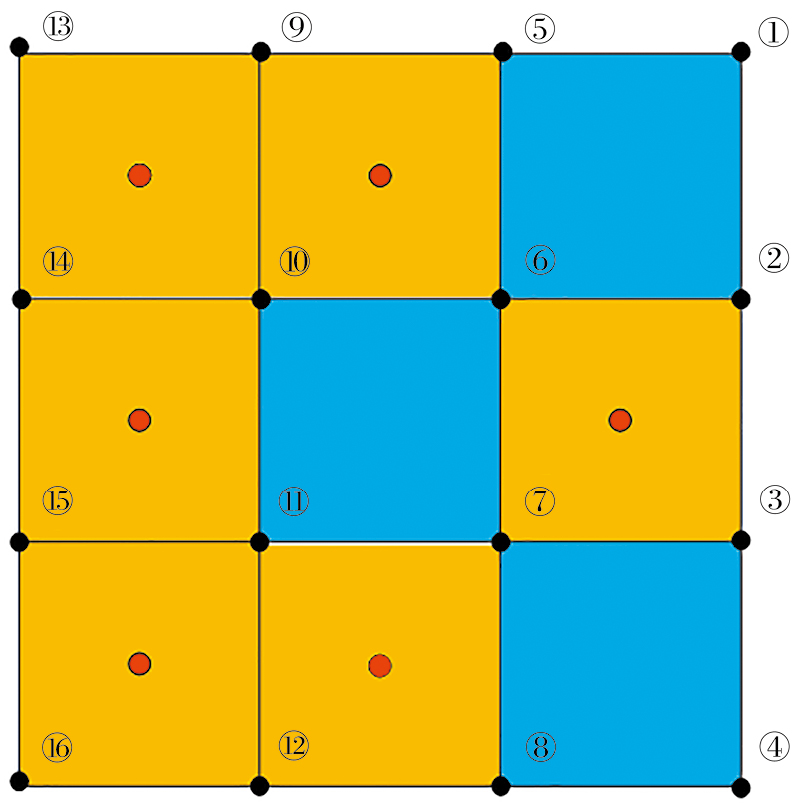
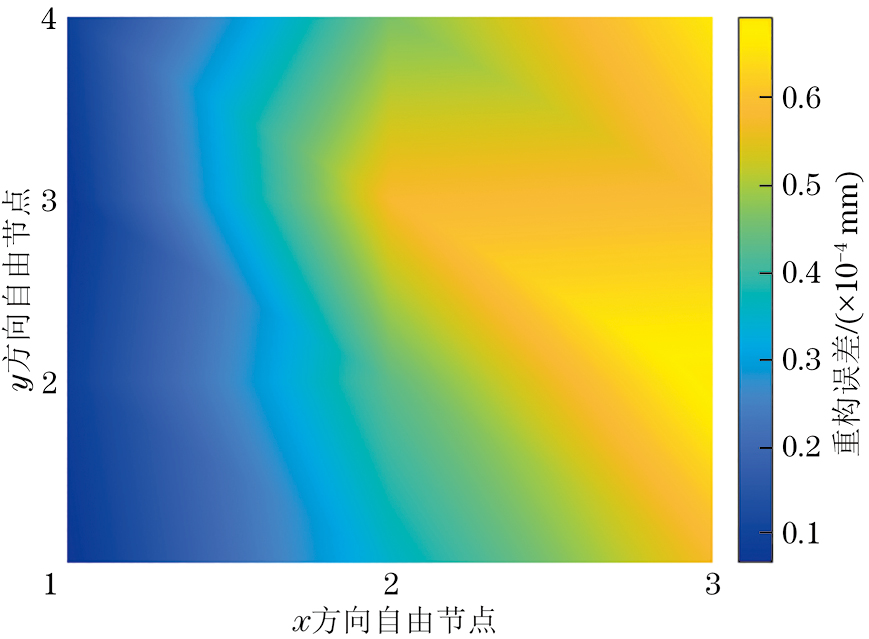
图9中红色各点代表的传感器布设方案为该双目标优化问题的最优解,可根据实际情况下对目标的侧重大小选择最优布设方案。根据上述优化结果,取C点代表的布设方案进行展示(见图10),其中黄色代表选择的单元位置,蓝色代表未被选中的单元位置,该方案下的节点位移重构数据如表4所示。进一步评估各节点的重构绝对误差,得到所有节点的位移绝对误差如图11所示。
| 节点编号 | 形状监测系统/mm | 激光测距仪/mm | 绝对误差/mm |
|---|---|---|---|
| 1 | 4.236 | 4.810 | 0.574 |
| 2 | 4.024 | 4.717 | 0.693 |
| 3 | 4.092 | 4.682 | 0.590 |
| 4 | 3.990 | 4.653 | 0.663 |
| 5 | 1.951 | 2.303 | 0.352 |
| 6 | 2.030 | 2.463 | 0.433 |
| 7 | 2.105 | 2.684 | 0.579 |
| 8 | 2.015 | 2.480 | 0.465 |
| 9 | 0.612 | 0.679 | 0.067 |
| 10 | 0.610 | 0.701 | 0.091 |
| 11 | 0.597 | 0.665 | 0.068 |
| 12 | 0.595 | 0.692 | 0.097 |
根据试验结果,所提算法在实际环境下的最大重构误差为0.693 mm,均方根误差为0.455 mm,节点位移误差相比仿真结果均偏大,但误差都在允许范围内。此外,节点的最大位移重构误差多位于远离约束端且未进行传感器布设的单元节点处,符合实际情况。
4. 无损检测证书挂证网结论
文章针对阵列天线变形监测需求,提出了一种基于逆有限元法的变形重构算法,通过理论推导和仿真分析,证明了逆有限元法的重构精度会随着单元划分网络的增加而提高;同时针对算法重构精度与应变传感点数量之间的矛盾,提出了一种多目标遗传算法优化逆有限元法的改进模型,并通过算法仿真和试验证明了基于多目标遗传算法改进的逆有限元法能在保证被测物体位移重构精度的同时,减少所需的应变传感器数量。研究结果在实际工程中,具有一定的应用意义