复合材料是通过专业的工艺将两种或两种以上具有完全不同机械性能、热学性能和电性能的材料组合而成,既能继承各组成材料的优点,又能实现它们之间性能的互补,进而具有更优的性能。目前,复合材料已在航空航天、建筑以及汽车电子等行业广泛应用[1]。
然而,复合材料在制备或使用过程中,材料内部可能会产生空洞、裂缝或者脱黏等损伤,这些损伤会破坏材料结构的整体性,进而严重影响材料的力学性能。复合材料的无损检测一般是指在不损害被检测对象使用性能的情况下,使用超声、红外或电磁等方法对被检测对象内部或表面缺陷进行检测[2]。笔者研究了基于电磁检测的复合材料缺陷电磁逆散射成像问题,该问题可以分为定量成像和定性成像两大类,其中定量成像需要求解未知散射体的相对介电常数分布,而定性成像则无需求解。考虑到实际生活中产生的此类损伤大多为连续的不规则形状,传统的定量电磁逆散射成像技术如伯恩近似迭代法、对比源反演法、子空间优化法等不仅无法实现精准重建,而且其复杂度高,无法实时成像[2-5]。近年来,深度学习发展快速,其在电磁逆散射问题上展现出了卓越的非线性拟合能力,是一种新的定量电磁逆散射方法,受到了广泛关注[6-8]。而时间反演法作为一种定性成像的代表性方法,虽然成像精度不高,但实现较为简便并且可以实时成像。文章主要基于这两种方法对复合材料内部复杂形状的损伤重建问题进行探讨。
时间反演算法最早由FINK于1992年提出并在超声领域得到了广泛的应用[9]。基于频域的矢量散射理论和并矢格林函数,CARMINATI等[10]在2007年将时间反演算法从超声波严格推广到了电磁波。微波时间反演并不是时间上的倒流,而是运动方向的倒转。基于波动方程的时间反转不变性,记录下激励源所发出的全部场,再将这些场进行时间反转处理,然后发射回检测区域,在初始源的位置处就可以得到一个聚焦点。CHEN等[11]指出边界的对称性可能导致TR电磁波出现多点聚焦或者连续聚焦。MUKHERJEE等[12-13]研究了微波时间反转算法用于检测复合材料和金属黏接层中单个和多个脱黏损伤的能力,提出了一种结合多个源的时间分辨信息重构简单扩展性损伤的方法,如直线型损伤。
根据模型的输入数据类型,使用深度学习解决电磁逆散射问题的方法大致可以分为间接反演法和直接反演法两大类[14]。间接反演法是指先借助其他传统电磁逆散射方法获得一个粗糙的轮廓,再使用深度学习方法学习从这一粗糙结果到精确轮廓之间的映射关系,进而获得一个较为精确的重构结果。WEI等[15]分析比较了原始散射场数据、BP算法生成的初步图像以及由主成分分析法获得的感应电流数据等三种不同数据作为深度学习模型U-Net的输入的效果,最后验证了使用主成分分析法作为U-Net的输入的性能要优于其他两种方案的性能。直接反演法是指直接将采集到的散射场信号作为深度学习模型的输入来重建计算域的相对介电常数或其他电磁参数的分布。ZHANG等[16]基于卷积神经网络的编码器-解码器结构提出了一种新的深度学习模型,该模型可以直接利用采集到的散射场信号重构出计算域的相对介电常数分布。SONG等[17]提出了一种基于物理的深度学习模型uSOM-Net,引入了完整的物理损失函数来减轻电磁逆散射问题的不适定性。SALADI等[18]提出了一种两阶段深度学习方案来解决电磁逆散射问题,该方法首先使用DConvNet模型从散射场信号中提取特征,然后使用Attention U-Net模型来优化重建的图像。
目前基于深度学习的电磁逆散射方法大多仅考虑损伤位于自由空间且由环状天线阵列包围计算域时的这类理想情况,而基于时间反演的电磁逆散射方法大多仅讨论点状或直线形等较为理想的损伤。考虑工程实际,笔者主要研究在复杂背景介质(如复合材料)中具有复杂形状的损伤重建方法,基于二维时域有限差分算法对带有金属背板的复合材料模型进行了数值仿真,分别使用微波时间反演算法和深度学习方法对复合材料内部的复杂形状损伤进行了重建,在此基础上提出了TR-Unet方法,实现了对带有金属背板的复合材料内部具有复杂形状的扩展性损伤的高效精确重建。
1. 方法论述
微波无损检测方法一般分为正问题和逆问题两部分。正问题一般是指使用经典数值方法如矩量法(MoM)、时域有限差分方法(FDTD)或者有限元法(FEM)来模拟电磁波在介质中的变化,而逆问题是指使用天线阵列接收到的散射场信号来重建计算域的相对介电常数或其他物理特性的分布情况。笔者使用时域有限差分方法对复合材料进行正问题的数值仿真,再利用天线阵列接收到的散射场信号,分别使用时间反演算法和深度学习算法来求解逆问题。
1.1 FDTD基本原理
考虑二维情况下TMz模式的FDTD方法,假设磁场只在x和y方向上随时间变化,电场只在z方向上随时间变化,材料为无耗媒质,则基于法拉第电磁感应定律和安培环路定律,在点处,进行空间和时间上的离散化,可以得到
| Hq+12x(m,n+12)=Hq−12x(m,n+12)-ΔtμΔy[Eqz(m,n+1)-Eqz(m,n)] | (1) |
| Hq+12y(m+12,n)=Hq−12x(m+12,n)+ΔtμΔx[Eqz(m+1,n)-Eqz(m,n)] | (2) |
| Eq+1z(m,n)=Eqz(m,n)+{ΔtεΔx[Hq+12y(m+12,n)-Hq+12y(m-12,n)]-ΔtεΔy[Hq+12y(m,n+12)-Hq+12x(m,n-12)]} | (3) |
式中:Hx为磁场在x方向的分量;Hy为磁场在y方向上的分量;m为x方向上的空间步数;n为y方向上的空间步数;q为时间步数;Ez为电场在z方向上的分量;材料参数μ和ε分别为各离散点处的磁导率和介电常数;Δx和Δy分别为x和y方向上的空间步长;Δt为时间步长。
1.2 时间反演算法基本原理
电磁场的标量波动方程为

式中:ϕ(r,t)为该方程的一个解,被称为发散波的解,表示从脉冲源辐射出的电磁波;ϕ(r,-t)也是该方程的解,被称为收敛波的解,表示从空间中收敛至脉冲源位置处的电磁波。
基于波动方程在无耗媒质和时不变媒质中的时间反转不变性,时间反演算法只需将源点发散出去的波在时间上进行反转得到时间反转电磁波,再发射回检测区域,时间反转电磁波就会自适应地聚焦于激励源所在的位置。
基于这一原理,为了使时间反转电磁波聚焦于损伤所在的位置,分别在有损伤和无损伤的复合材料模型中应用FDTD方法模拟电磁波的传播,然后将这两个模型中的传感器接收到的散射场信号相减,获得目标响应信号ϕp(r,t),由于此时损伤相当于次生源,将目标响应信号ϕp(r,t)在时间上进行反转并发射回健康模型,时间反转目标响应信号就会自适应地聚焦于损伤所在的位置,进而重构出损伤的形状。
显然,时间反转电场会在损伤处产生峰值,因此可以使用能量积分法作为成像算法,即使用式(5)对时间反转电场在总的时间步上进行积分,能量最大处即代表时间反转信号聚焦的位置[12]。

式中:W(x,y)为每个位置处的积分能量;Ez(x,y,t)为时间反转场中每个时间步上每个位置处的电场值;η(x,y)为每个位置处的本征阻抗;T为总时间。
而多个激励源的时间反演实际上是将不同位置处的源依次进行发射-回传操作,再对每个源的能量积分结果进行累加[13]。
1.3 U-Net模型原理
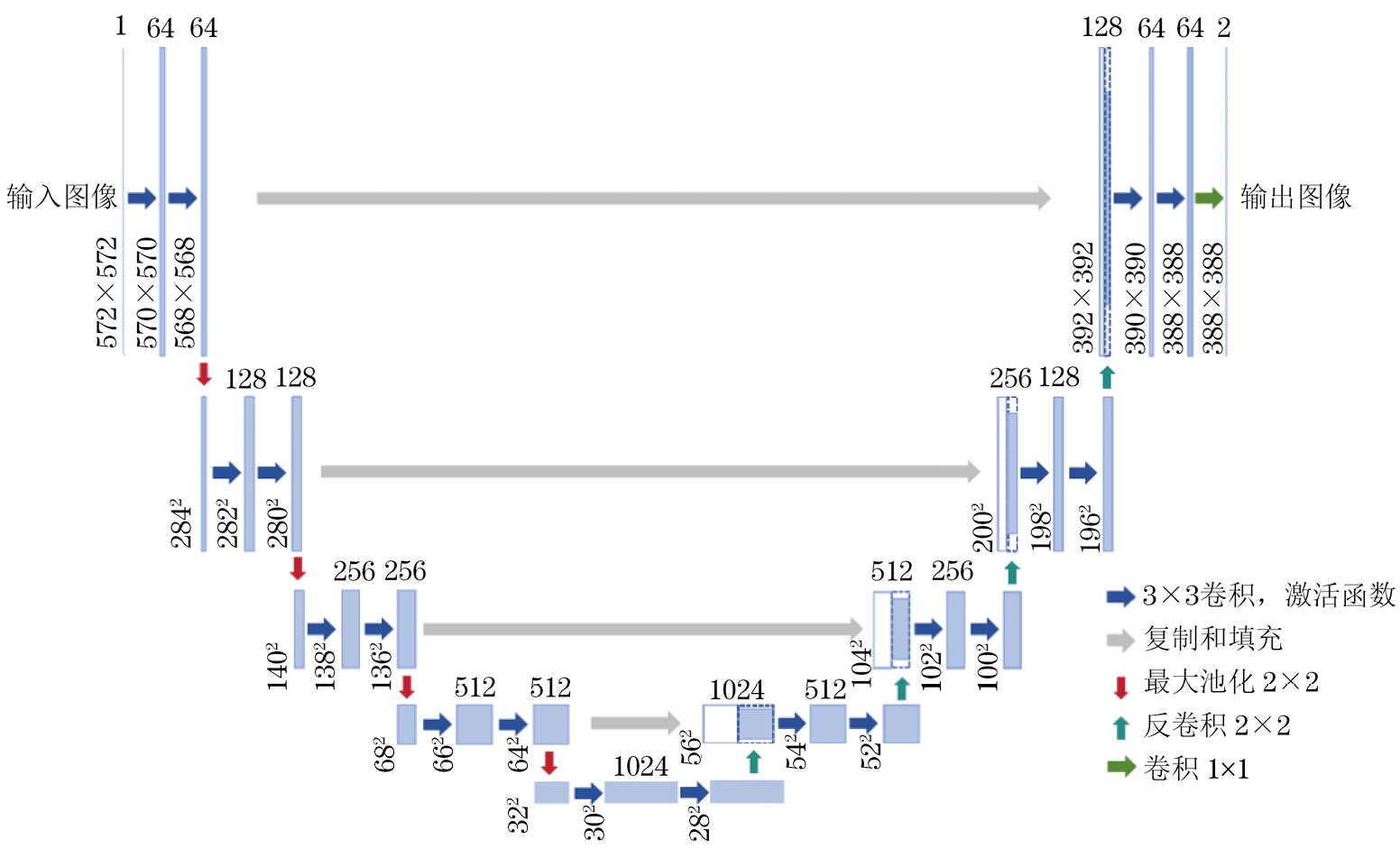
U-Net是一种用于图像分割的全卷积神经网络,能够实现像素级别的分类。文章使用的U-Net模型结构如图1所示。图1中的左侧是输入图像,经过两次卷积和池化操作后,得到64个特征通道,然后进行一次最大池化操作,实现下采样,将图像尺寸缩小为原来的一半。这个操作被重复4次,最终得到1 024个特征通道,完成下采样过程。图1中右侧的操作与左侧类似,只是将池化操作替换为反卷积操作以实现上采样。每进行一次上采样,图像尺寸扩大一倍,通道数减半。池化和反卷积操作会导致空间细节信息的丢失,因此在图像尺寸恢复的过程中,U-Net引入了跳跃连接(如图1中的灰色箭头),以弥补信息的丢失。尽管文中 U-Net 使用的是same卷积,但由于输入数据尺寸的影响,在下采样过程中可能会引入舍入误差,从而导致左右两侧同一层中的特征图尺寸不一致,无法直接进行拼接。所以,在跳跃连接时,需要先对左侧的特征图进行裁剪或对右侧的特征图进行填充(文章选择对右侧特征图进行填充),以确保其尺寸一致。最后,使用两个1×1卷积将64个特征通道转化为2个特征通道,实现二分类操作,将图像分为目标和背景两个类别,以区分材料和损伤。
此外,在直接使用散射场数据进行反演时,由于输入和输出的尺寸差异较大,输入图像即传感器采集到的差值信号的尺寸为T×M(长×宽),其中T为FDTD仿真的总时间步长,M为传感器的数量,而输出图像的尺寸为检测区域的大小G×G(长×宽),其中G为检测区域在x轴或y轴方向上的网格数量。因此,在将图像输入U-Net模型之前,文章进行了填充和最大池化操作,将输入图像的尺寸调整为G×G。而使用时间反演的结果作为U-Net模型的输入数据时,由于输入输出数据尺寸一致,而无需进行此操作。
2. 数值仿真
2.1 试验设置
2.1.1 材料模型及FDTD仿真设置
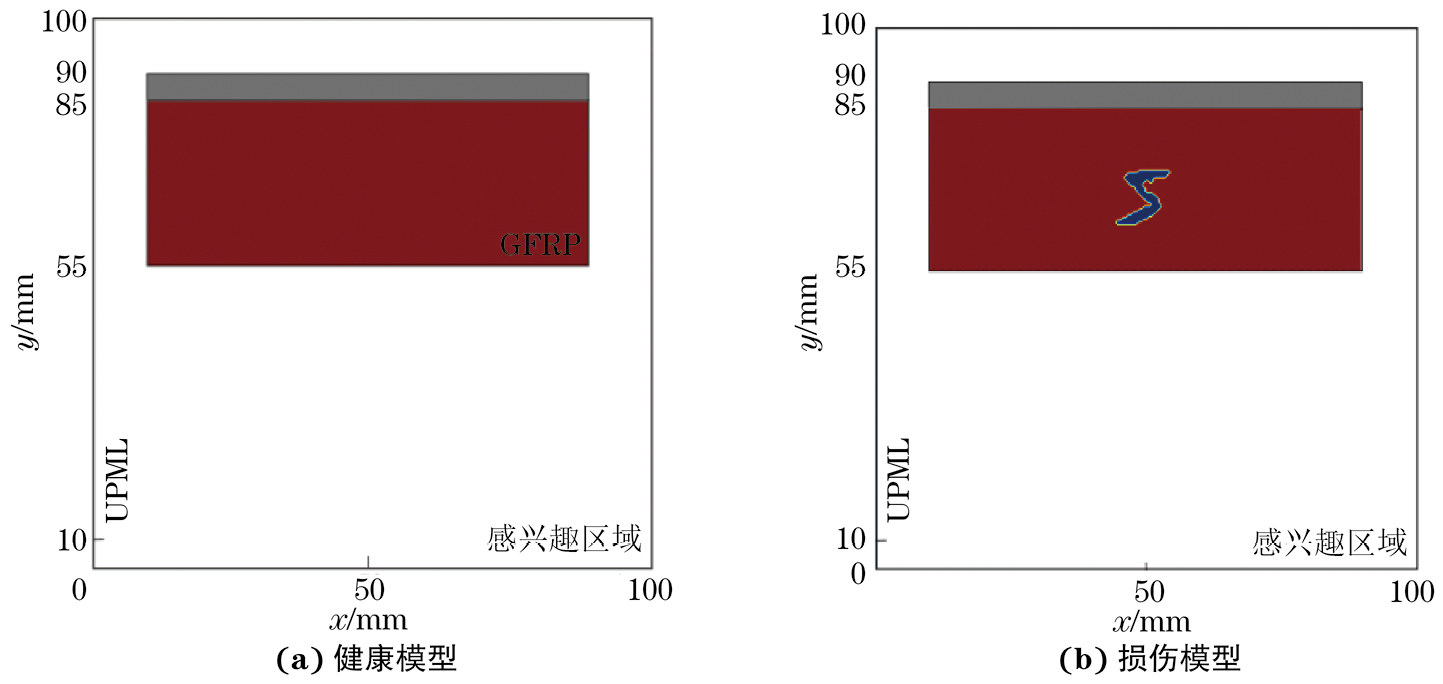
数值仿真中使用的材料模型结构示意如图2所示,复杂形状的埋藏损伤[即图2(b)中蓝色数字“5”]设置在材料区域内(即图2中红色部分),损伤假定为空气,其相对介电常数设置为1。检测区域的大小为100 mm×100 mm(长×宽),复合材料由玻璃纤维增强聚合物(GFRP)构成,其相对介电常数为4.6,尺寸为100 mm×30 mm(长×宽),材料上方紧贴一层金属背板(即图2中灰色区域),其尺寸为100 mm×5 mm。在边界上使用单轴各向异性完全匹配层(UPML)作为吸收边界条件。
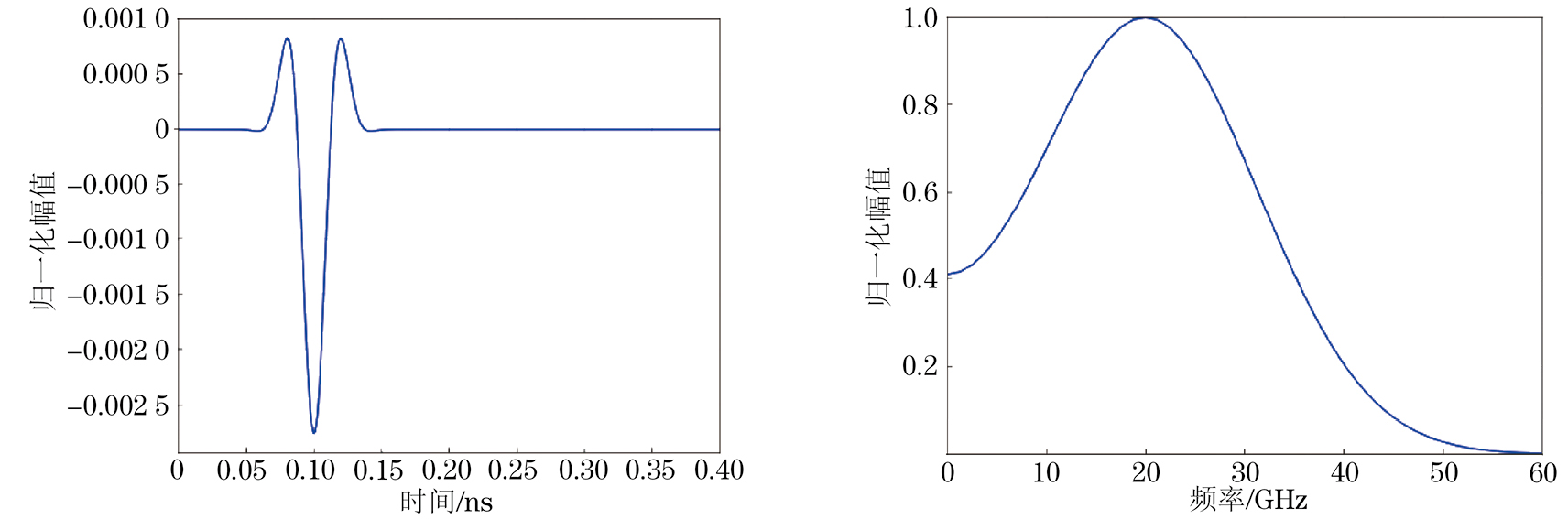
激励源使用调制高斯脉冲,以电流源的形式添加到发射天线上,其中心频率f0为20 GHz,脉冲宽度为20 ps,激励源的时域和频域波形如图3所示。